Introduction
Inside a Stirling engine is transformed heat to work through a closed heat cycle. The internal work of the engine, torque and others engine parameters can be predicted through p-V diagram, respectively p-φ diagram, where φ is angle of rotation of crankshaft. An accuracy of these computations is directly proportional to a similarity of shape of the designed cycle to real Stirling engine cycle. The Stirling engine cycle, which is described here is based on several types of heat cycles used to calculation of the Stirling engine cycle, because these cycles have common features (so called assumptions of solving).
Working pressure equation
Working pressure
Working temperature
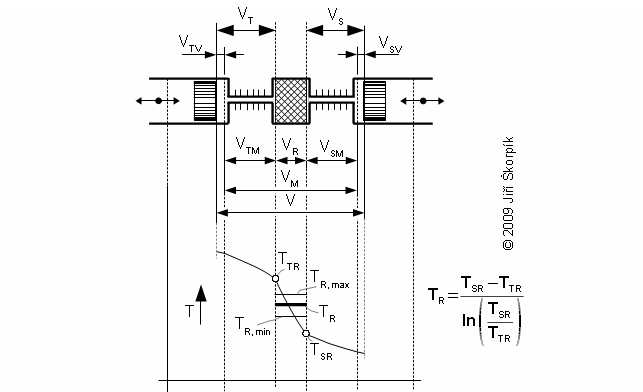
Temperature inside regenerator
Working pressure inside the engine is changed under a change of temperature and a volume of the working volume. From description of the Stirling engine can be the working volume separated to three volumes, the death volume VD, the cylinder volume on the hot side engine VHV and the cylinder volume on the cold side engine of the engine VCV. The mean working temperature in all volumes is being varied during one cycle between their maximum value and their minimum value, see Figure 1.
Simplifying assumptions
Temperature ratio
Working pressure
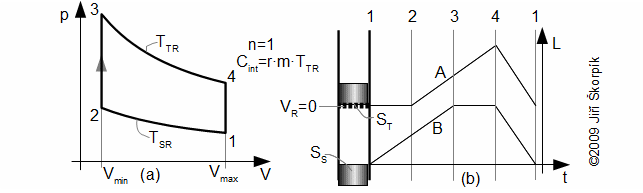
Reduced volume
The calculation of the Stirling engine cycle, which is described here is can use under these simplifying assumptions: (1) Value of mean polytropic index of thermodynamics processes inside working volumes of engine is the same during one cycle. – (2) Temperature ratio at border of regenerator is constant, τ=THR/TCR=const. – (3) There is no pressure loss, pressure of working gas is same in all working volumes. (4) Working gas is ideal gas. – (5) Stirling engine is perfect sealed. – (6) Stirling engine cycle is steady (the same cycle is repeated). Under these simplifying assumptions, Equation 2 can be derived to calculate engine pressure as function of the working volume.
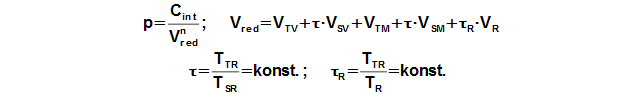
Constant of engine
The integration constant CE can be computed from any point of cycle, in which be knownworking pressure (for expample required mean working pressure) and a value of reduced volume, see Equation 3.
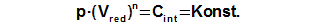
Polytropic index
The polytropic index inside the Stirling engine may be in the interval <1; κ>; (κ [1] heat capacity ratio – adiabatic index) for steady cycle. The polytropic index can not be less than 1. If n is equal κ, then an engine is perfectly thermally isolated and between the hot and cold side of the engine can not occur temperature difference (τ is equal 1 and internal work of the engine is zero). In case n=1 only isothermal processes are performed in the engine, therefore the isothermal processes can be regarded as comparative processes for real processes.
Isothermal ratio
The isothermal ratio determines (see Equation 4) how much polytropic process inside the working volume is similar to isothermal process. Its value can be in interval <0; 1>. If value of isothermal ratio is 1, then thermodynamic process inside the working volume is isothermal process. If value of isothermal ratio is 0, then thermodynamic process in the working volume is adiabatic process. The difference κ-1 is the maximum deviation between polytropic process and isothermal process inside the working volume.
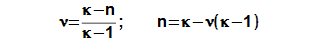
Isothermal ratio values
The isothermal ratio about 0,5 is the usual value for engines with ideal heat transfer between the working gas and heat flow area (e.g. Strojírny Bohdalice Stirling engines, United Stirling V160). The isothermal ratio smaller than 0,5 is the usual value for engines with small heat flow area, higher speed, small death volumes. The isothermal ratio bigger than 0,5 is the usual value for engines with bigger heat flow area, small speed, bigger death volume or engines with control heat flow (difficult to achieve). Polytropic index is function engine speed, engine geometry and working gas.
Working volumes at crankshaft engine
Crankshaft engine
The motion of the piston is often performed through a crankshaft, then the volumes of the engine are function of an angle of rotation φ, length of crank r and length connecting rod c, see Figure 5 and Equation 6.
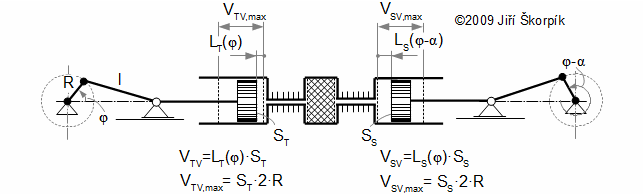
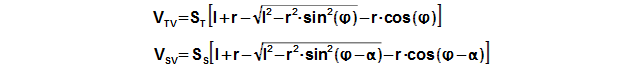
Through these equations be can calculating the reduction volume Vred of engine.
Mean working pressure
The mean pressure of cycle be computed according to the mean value theorem which is applied on function p(φ), see Equation 7.
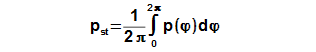
If the enter of calculation contains the mean working pressure of cycle then CE can be determined through iteration from result Equation 7.
Working pressure profile
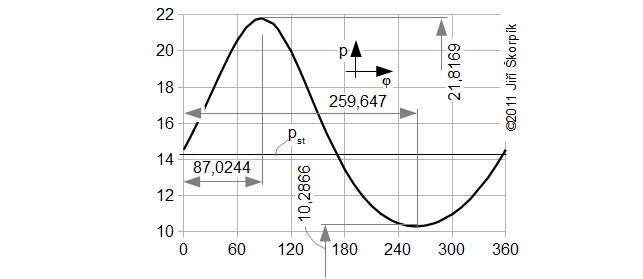
Working temperature equations
Working temperature
If n≠1 then temperature of the working gas is changed inside individual volumes according equations:
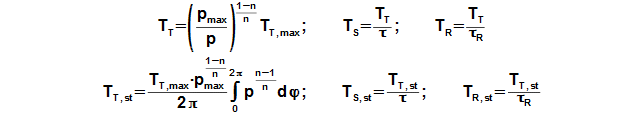
Mean temperature
From these equations is evident, that temperature change follows pressure change and this change is the bigger the bigger is the mean temperature of the working gas in the individual volume. If mean temperature of the working gas is known only, then for a calculation of the temperature THR,max be must used iteration calculation. It means that during first step of the calculation be must estimate of THR,max and by the Equation 8 computes the temperature THR,mean. This result must be equal with the required mean temperature on hot side the engine.
Working temperature profile
Stirling cycle and Schmidt cycle
Stirling cycle
Schmidt cycle
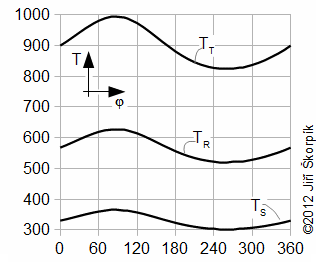
The Stirling cycle and a Schmidt cycle are simplified Stirling engine cycles with assumtion n=1.
Stirling cycle
The Stirling cycle (Figure 9) assumes linear motion of pistons and zero death volumes.
Schmidt cycle
Gustav Schmidt
The Schmidt cycle assumes sinusoidal move of pistons (c=0, see Equations 10) and non-zero death volumes – Gustav Schmidt (1826-1881), professor at German Polytechnic in Prague. He published his cycle at 1871. Details about these cycles are shown in [Škorpík, 2008], [Walker, 1985]. On
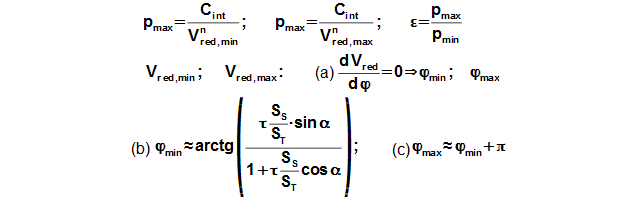
Other comparative cycles for Stirling engine
Theodor Finkelstein
Israel Urieli
David Berchowitz
Theodor Finkelstein be published cycle where n=κ, this cycle be computed by Finite element methods [Walker, 1985], [Martini, 2004, p. 87]. The most widely is cycle with adiabatic processes in cylinders and isothermal processes in death volumes. Authors this cycle are Israel Urieli and David Berchowitz [Urieli and Berchowitz, 1984] (authors assembled set of differential equations, which are solved by Runge – Kuttak method).
References
Citation this page
Copyright©Jiří Škorpík, 2012
All rights reserved.