Copyright©Jiří Škorpík, 2006-2022
Všechna práva vyhrazena.
Síly působící od proudu tekutiny na plochy stroje lze určit z věty o změně hybnosti. Její speciální tvar se používá i k výpočtu sil působící na lopatky v lopatkové mříži od proudu tekutiny, což je klasická úloha v lopatkových strojích.
Síly působící od proudu tekutiny na plochy stroje lze určit z věty o změně hybnosti (druhý Newtonův zákon). Podle věty o změně hybnosti je změna hybnosti tekutiny v čase rovna součtu vnějších sil působící na tekutinu v kontrolním objemu. V případě aplikace tohoto zákona na tekutinu uzavřené v kontrolním objemu VC (Obrázek 1) připadají v úvahu jako síly vnější: tlakové síly od okolní tekutiny na hranicích kontrolního objemu Fp, tíha tekutiny v kontrolním objemu Fh, a síly působící od těles uvnitř a na hranicíh kontrolního objemu Fb. Změna hybnosti tekutiny uvnitř kontrolního objemu je také rovna rozdílu součinu rychlosti a hmotnostního toku mezi vstupem a výstupem z kontrolního objemu [Bathie, 1984], [Kadrnožka 2003].

Při výpočtu sil působící na lopatky lopatkového stroje jsou při defininování hranic kontrolního objemu cílem takové hranice, na kterých jsou známy hodnoty parametrů nutné pro výpočet pomocí věty o změně hybnosti. Proto je kontrolní objem na Obrázku 2 vymezen tak, aby procházel středem lopatkového kanálu, respektive hranice AD a BC byly od sebe vzdáleny o rozteč lopatek1.. Hranice AD a BC jsou očekávané proudnice relativních rychlostí W rychlostního trojúhleníku1. této lopatkové mříže. Lopatkové kanály jsou v jedné lopatkové mříži stejné, takže působení tlakových sil na hraních AB se vyruší s působením tlakových sil na hranicích DC. Na těchto hranicích se vyruší i hodnota integrace součinu absolutní rychlosti V a hmotnostního toku, viz Rovnice 2.

Typické pro vyšetření sil ve stupni lopatkového stroje je použití válcové soustavy souřadnic. Síla F ve válcové soustavě souřadnic1. má tři prostorové složky, a to složku v radiálním směru Fr, v obvodovém směru Fθ (tato síla vytváří kroutící moment) a v axiálním směru Fa (způsobuje namáhání rotoru v axiálním směru a zachycuje jí axiální ložisko) – zkráceně se označují tyto složky síly jako radiální, obvodová a axiální síla.
Síla působící na lopatku je přibližně kolmá na střední aerodynamickou rychlost v lopatkové mříži Wm, která je střední rychlostí relativních rychlostí na vstupu W1 a výstupu W2. Respektive lze dokázat (viz Rovnice 3), že výsledná síla působící na lopatku od proudu nestlačitelné tekutiny F je kolmá na střední aerodynamickou rychlost wm při proudění beze ztrát.

Při návrhu rozložení energie, respektive její transformace ve stupni lopatkového stroje se vychází ze dvou směrů. Ve směru kolmém na meridánový směr1. se navrhuje rozložení Eulerovy práce, což je lokální hodnota vnitřní práce. V meridiánovém směru rozhoduje o vlastnostech stupně návrh stupně reakce, který popisuje rozdělení energetických transformací mezi stator a rotor stupně.
Eulerova práce nebo obvodová práce je prací tekutiny předaná lopatkám v okolí vyšetřované proudnice, viz Obrázek 4(b). Rozdíl oproti vnitřní práci1. stupně wi je v tom, že vnitřní práce stupně je průměrná hodnota práce veškeré pracovní tekutiny, která protéká stupněm (včetně mezer) a lze ji určit z kompletní energetické bilance stupně, viz Obrázek 4(a). Takže část tekutiny vykoná větší Eulerovu práci než jiná, ale jejich průměr je wi. U reálných stupňů je nevětší Eulerova práce v jádru proudu (na středním průměru lopatek), kde jsou nejmenší ztráty. Naopak u okrajů lopatek, respektive v blízkosti jejich pat a špic, je Eulerova práce nejmenší kvůli vysokým ztrátám třením a vnitřní netěsností. Eulerovu práci lze stanovit z rychlostních trojúhleníků na vyšetřované prouděnici, viz Rovnice 4(c) – Eulerova turbínová rovnice.

Podobným způsobem lze stanovit dvěma cestami účinnost stupně, buď k Eulerově práci (tzv. Eulerova účinnost, respektive obvodová účinnost) nebo vnitřní práci (tzv. vnitřní účinnost stupně), jako je provedeno v Úloze 4.
Stupeň reakce je definován jako poměr mezi změnou statické entalpie v rotorové řadě lopatek a změnou celkové entalpie stupně (Vzorec 5), či změnou statické entalpie stupně – zaleží na zvyklosti [Kadrnožka, 2004], [Japikse, 1997], [Bathie 1984], [Ingram, 2009]. Popisuje tedy rozložení energetické transformace mezi statorovou a rotorovou řadou lopatek stupně.

Stupeň reakce se stanovuje ke konkrétnímu proudovému vláknu (poloměru) podobně jako Eulerova práce. Pro výpočet stupně reakce je důležitá znalost konstrukce h-s diagramu, ze kterého lze určit rozdíly měrných entlapií Δhs a ΔhR (viz Úloha 5, Úloha 6). h-s diagramy a popis jejich konstrukce jsou uvedy na Obrázku 6. V případě hydraulických strojů lze stanovit požadované rozdíly tlaků Δps a ΔpR i z Bernoulliho rovnice pro relativní proud, viz Úloha 7 a Úloha 6.

Většina stupňů je navrhována s proměnným stupněm reakce po výšce lopatek, přitom častým požadavkem při konstrukci stupně je stupeň reakce na středním poloměru kolem 0,5 (u radiálních stupňů i něco vyšší kvůli rozdílu obvodových rychlostí na rotoru), protože při maximální Eulerovy práci jsou absolutní rychlosti ve statorových kanálech přibližně stejné jako relativní rychlosti v rotorových kanálech, a tedy i rozložení ztrát mezi stator a rotor je rovnoměrné, viz Obrázek 7.

Nulový nebo jen velmi malý stupeň reakce mají Lavalovy turbíny1. a Peltonovy turbíny. Z pracovních strojů se používají nízké stupně reakce u některých typů ventilátorů. Při malém stupni reakce je tlaková síla působící na rotor také malá a proto se tyto stupně označují jako rovnotlakové nebo akční. Naopak na rotory stupňů s významným stupně reakce působí i větší tlaková síla na rotor a proto se označují jako přetlakové nebo reakční.
U axiálních stupňů se zvyšujícím stupněm reakce klesá prohnutí lopatek (klesá potřebná změna hybnosti) a tedy i jejich citlivost na odtržení proudu od profilu.
Rovnice ideálního proudění jsou odvozeny pro proudění ideálních tekutin bez vnitřních ztrát. I když se jedná o rovnice ideálního proudění, tak jsou klíčové pro základní návrh průtočných částí lopatkových strojů, predikci vlastností, analýzu vlivu tvaru průtočných částí na vnitřní ztráty stroje, pochopení příčin hávarií nebo problémového chodu lopatkových strojů.
Základními rovnicemi popisující rychlosti ideálního proudění jsou rovnice potenciálního proudění. Proudění je považováno za potenciální (znamená to, že rychlost lze vypočítat pouze pomocí souřadnic bodu podle potenciální funkce V=f(x, y, z) v případě pravoúhlé soustavy souřadnic, nebo podle funkce V=f(r, θ, a) v případě válcové soustavy souřadnic, kdy takové proudění označujeme jako osově symetrické potenciální proudění. Další veličiny ideálního proudění lze vypočítat z energetických rovnic a Eulerovy rovnice hydrodynamiky.
Pokud má být proudění potenciální, pak musí být rotor vektoru rychlosti v celém vyšetřovaném objemu roven nule, Rovnice 8(a). Aby proudění bylo považováno za osově symetrické, tak musí mít gradienty složek rychlosti v obvodovém směru ve valcové soustavě souřadnic rovny nule, viz Rovnice 8(b), protože obvodové souřadnice jsou uzavřené a rychlost v počátku osy obvodového směru musí být totožná s tou na konci souřadnic – jedná se o stejný bod, současně je tato rychlost nezávislá na stanovení počátku osy obvodového směru. Z těchto podmínek lze odvodit speciální Rovnice 8(c-h) pro rychlost, ale uvedené podmínky lze aplikovat i na další veličiny pracovní tekutiny.
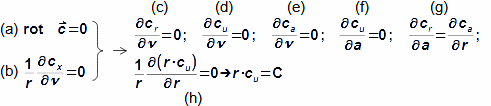
Součin r·Vθ se nazývá cirkulace obvodové složky rychlosti, která je konstatní, takže má stejné vlastnosti jako potenciální vír [Škorpík, 2023, s. 1.40]. Jestliže je cirkulace konstantní, pak i rozdíl cirkulací před a za rotorem je konstantní a pak i podle rovnice Eulerovy práce (Rovnice 4) bude Eulerova práce potenciálního proudění konstantní po výšce lopatek, viz Úloha 8.
Rovnice osově symetrické potenciálního proudění lze aplikovat i na spirální dráhy, například ve spirálních kanálech (Úloha 9) nebo v bezlopatkových difuzorech a konfuzorech (Úloha 10).
Při výpočtu další stavových veličin lze použít velmi efiktivně i Eulerovu rovnici hydrodynamiky pro potenciální proudění, například článek Vnitřní tření tekutiny a vývoj mezní vrstvy [Škorpík, 2023b]. Z této rovnice lze mimo jiné vyčíst, že gradient tlaku potenciálního proudění bez vliv gravitačního zrychlení nemůže mít obvodovou složku, protože ji nemá ani gradient rychlosti, respektive kinetické energie, viz Úloha 8.
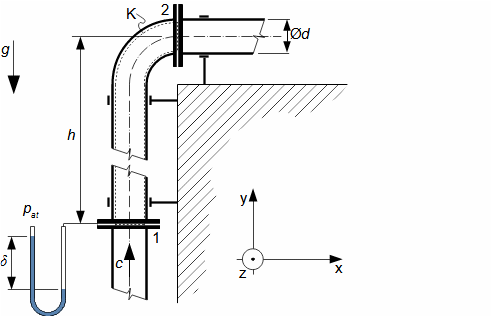
| 1: | zadání: | d; z; zH2O; V | 4: | výpočet: | Fh,x; A; m; p1; p2; Fp,x; Fx | |||||||
| 2: | odvození: | rovnic pro Fx; Fy; Fz | 5: | výpočet: | VC; m; Fh,z; Fpz; Fz | |||||||
| 3: | odečet: | ρ; g; pat | 6: | výpočet: | Fy |

| 1: | zadání: | m; p1; z; r1; r2; V1; V2; α2; b | 2: | výpočet: | V2r; Fr,p; Fr | |||||||
| 3: | výpočet: | V2θ; Fθ | 4: | výpočet: | F |

| 1: | zadání: | rt; rh; V1θ; Va; V2; N; z | 4: | výpočet: | rm; U; -W2θ; W1θ; Wmθ; Wm; βm; ε; Fa; F | |||||||
| 2: | odečet: | ρ | 5: | odečet: | pat; g | |||||||
| 3: | výpočet: | A1; A2; Q; m; Fθ | 6: | výpočet: | V1; p1; p2 |

| 1: | zadání: | Δhis; Lw; V1; W2; V0; V2; W1; U1; U2 | 3: | výpočet: | wi | |||||||
| 2: | výpočet: | wE | 4: | výpočet: | wis; ηE; ηi |

| 1: | zadání: | V1; V2; W1; W2 | 3: | výpočet: | wE; Δhs; R | |||||||
| 2: | výpočet: | ΔhR |

| 1: | zadání: | Δps; ρ; U2; U1 | 3: | výpočet: | ΔhR; R | |||||||
| 2: | výpočet: | Δhs |

| 1: | zadání: | r1; V1; V2; N; α1; Δz | 4: | odvození: | rovnice pro ΔpR | |||||||
| 2: | odvození: | rovnice pro Δps | 5: | odečet: | g; Lw,0-2; Lw,1-2 | |||||||
| 3: | výpočet: | U1; V1θ; wE | 6: | výpočet: | R |

| 1: | zadání: | wE; rt; rh; N; Va; V2; p2; ρ | 6: | výpočet: | p1h; p1m; p1t | |||||||
| 2: | výpočet: | rm; Uh; Um; Ut; V1θh; V1θm; V1θt | 7: | výpočet: | Δps; ΔpRh; ΔpRm; ΔpRt; Rh; Rm; Rt | |||||||
| 3: | výpočet: | V1h; V1m; V1t; α1h; α1m; α1t | 8: | odvození: | rovnice pro grad p1 | |||||||
| 4: | výpočet: | W1θh; W1θm; W1θt; W1h; W1m; W1t; β1h; β1m; β1t | 9: | odvození: | rovnice pro Δp1 | |||||||
| 5: | výpočet: | W2h; W2m; W2t; β2h; β2m; β2t |

| 1: | zadání: | R; r3; r2; r1; b2; b1; Δps; N; Q; p1s; ρ | 5: | výpočet: | p3s; V3θ; V3r; V3; p3 | |||||||
| 2: | odvození: | rovnice pro rθ | 6: | důkaz: | α=konst. | |||||||
| 3: | výpočet: | wE; U2; V2θ; C | 7: | diskuze: | o vlivu tření | |||||||
| 4: | výpočet: | rθ pro vybrané θ | 8: | diskuze: | rozložení rychlosti a tlaku na výstupu z hrdla |

| 1: | zadání: | V2θ; V2r; r2; p2; ΔpS; t2 | 4: | řešení: | r3 z m2=m3 | |||||||
| 2: | odečet: | h3; t3 z h-s diagramu | 5: | výpočet: | α2; α3 | |||||||
| 3: | výpočet: | V3; ρ3 | 6: | porovnání: | α2 vs α3 |