Oběh Stirlingova motoru

Škorpík, Jiří

34. Oběh Stirlingova motoru

Autor: Jiří Škorpík, skorpik.jiri@email.cz

Ve Stirlingově motoru probíhá uzavřený tepelný oběh, pomocí něhož se transformuje teplo na práci. Z návrhu tepelného oběhu motoru v p-V diagramu lze přibližně vypočítat vnitřní práci motoru, kroutící moment a další parametry. Přesnost těchto výpočtů je přímo úměrná tomu jak blízké jsou skutečné termodynamické děje probíhající v motoru dějům, které jsou použity pro konstrukci tepelného oběhu motoru. Oběh Stirlingova motoru, který je zde popsán vychází z několika typů oběhů používaných pro výpočet oběhu Stirlingova motoru, protože tyto oběhy mají společné znaky (tzv. zjednodušující předpoklady).

Tlak ve Stirlingově motoru

Tlak pracovního plynu v pracovním objemu Stirlingova motoru se během oběhu mění se změnou teploty a objemu pracovního objemu. Podle schématu Stirlingova motoru lze pracovní objem motoru rozdělit do tří objemů, mrtvý objem, objem válce na teplé a studené straně motoru. Střední teplota pracovního plynu v jednotlivých objemech se během jednoho cyklu může měnit mezi maximální a minimální hodnotou:

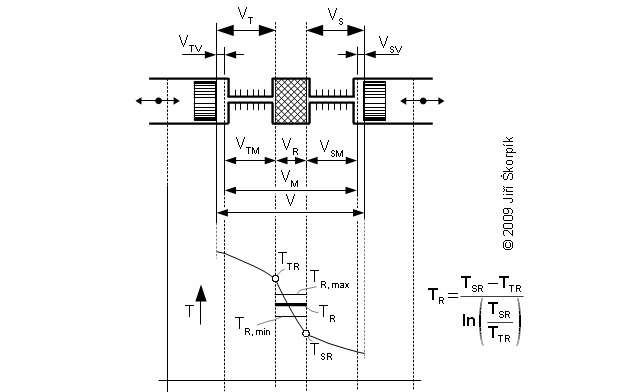
1.436 Teploty pracovního plynu.

T [K] teplota; V [m³] objem. Index _T označuje teplou stranu motoru; index S označuje studenou stranu motoru; index V označuje objem válce; index M označuje mrtvý objem; index R označuje objem regenerátoru; index TR označuje rozhraní mezi teplou stranou motoru a regenerátoru; index SR označuje rozhraní mezi studenou stranou motoru a regenerátoru. Odvození rovnice střední teploty pracovního plynu v regenerátoru je v Příloze 436 nebo [2, s. 69].

Výpočet oběhu Stirlingova motoru, který je zde popsán lze použít za určitých zjednodušujících předpokladů: (1) Střední hodnota exponentu polytropy termodynamických změn uvnitř pracovního objemu motoru je konstantní po celý oběh. (2) Teplotní poměr na hranici regenerátoru je konstantní τ=T_TR/T_SR=konst. (3) V celém pracovním objemu motoru je stejný tlak (neprobíhá žádná tlaková ztráta při proudění plynu). (4) Pracovní plyn je ideální plyn. (5) Pracovní objem je dokonale těsný. (6) Oběh je ustálený.

Z uvedených předpokladů řešení lze odvodit rovnici pro tlak pracovního plynu v motoru jako funkci jeho objemu:

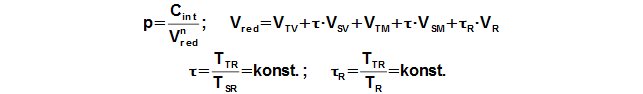
2.437 Tlak pracovního plynu ve Stirlingově motoru v závislosti na objemu motoru.

p [Pa] tlak pracovního plynu v motoru; C_int [Pa·m³] integrační konstanta; n [-] střední hodnota exponentu polytropy (exponent polytropy se během oběhu ve skutečnosti mění); τ [-] teplotní poměr na hranici regenerátoru; τ_R [-] teplotní poměr mezi teplotou na teplé straně regenerátoru a střední teplotou v regenerátoru; V_red [m³] redukovaný objem. Odvození rovnice je v Příloze 437, odvození je provedeno pro jednorozměrné proudění ideálního plynu. Tato rovnice byla poprvé zveřejněna v [4], [5].

Z rovnice je zřejmé, že průběh tlaku je především závislý na teplotách na hranicích regenerátoru, nikoliv na teplotách ve válcích. K chodu motoru je nutný teplotní rozdíl mezi teplou a studenou stranou.

Fyzikální interpretace integrační konstanty je patrná po formální úpravě rovnice tlaku:

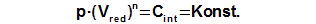3.438 Fyzikální interpretace integrační konstanty.

Integrační konstantu lze vypočítat z jakéhokoliv bodu oběhu, ve kterém je znám tlak a velikost redukovaného objemu.

Exponent polytropy a stupeň izotermizace

V ustáleném stavu může být exponent polytropy ve Stirlingově motoru v intervalu <1; κ> (κ [-] exponent adiabaty). Exponent polytropy nemůže být menší jak 1. Je-li n rovno κ, potom je motor dokonale tepelně izolovaný a mezi teplou a studenou stranou motoru nemůže vzniknout teplotní gradient (τ je rovno 1 a vnitřní práce motoru je nulová). V případě n=1 probíhají v motoru pouze izotermické děje, a izotermický děj lze považovat i za porovnávací vůči skutečným dějům:

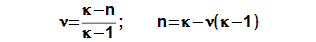4.446 Střední hodnota exponentu polytropy motoru.

ν [-] stupeň izotermizace*.

*Stupeň izotermizace: Stupeň izotermizace určuje jak moc je polytropický děj v daném objemu blízko izotermickým změnám. Jeho hodnota může být v intervalu <0; 1>. Čím blíže je hodnota poměru ν hodnotě 1, tím blíže je děj probíhající v daném objemu izotermickému ději, a naopak čím blíže je hodnota poměru ν hodnotě 0, tím blíže je děj probíhající v daném objemu adiabatickému ději. Rozdíl κ-1 je maximální možná odchylka polytropického děje v motoru od izotermického děje.

U motorů s ideálním sdílením tepla mezi pracovním plynem a stěnami motoru (např. motory Strojíren Bohdalice, United Stirling V160) se stupeň inzotermizace pohybuje kolem hodnoty 0,5. U motorů s malou teplosměnnou plochou, vyššími otáčkami, malými mrtvými objemi se stupeň izotermizace menší než 0,5. U motorů s velkou teplosměnnou plochou, malými otáčkami, velkým mrtvým objem nebo u motorů s řízeným tepelným tokem (obtížně realizovatelné) je stupeň izotermizace větší jak 0,5. Celkově je tedy hodnota exponentu polytropy funkcí otáček motoru, geometrie motoru a druhu pracovního plyn.

Naměřený stupeň izotermizace může ukázat na konstrukční nedostatky motoru.

Teplota, množství pracovního plynu, vnitřní práce motoru, přivedené teplo, odvedené teplo a regenerované teplo oběhu se vypočítá pomocí rovnic z článku 35. Energetická bilance oběhu Stirlingova motoru.

Změna tlaku ve Stirlingově motoru s klikovým mechanismem

Nejčastěji je pohyb pístů realizován pomocí zalomené hřídele, potom jsou objemy motoru funkcí pootočení hřídele φ (p – φ diagram) (V_TV(φ); V_SV(φ)):

5.439 Kinematika pístů pro případ α-modifikace Stirlingova motoru.

φ [rad] pootočení hřídele; α [rad] úhlové zpoždění pohybu pístu na studené straně za pohybem pístem na teplé straně; R [m] rameno kliky; l [m] délka ojnice; L [m; %] poloha pístu na teplé straně T a na studené straně S; S [m²] průřez válce na teplé straně T a na studené straně S.

V tomto případě lze, pro výpočet polohy pístu, použít rovnice polohy pístu spojeného s klikovým mechanismem:

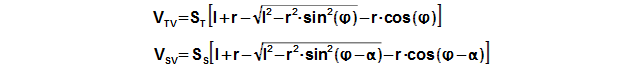
6.440 Objemy válců v závislosti na pootočení hřídele.

Kombinací Rovnice 2 a rovnic Rovnice 6 vznikne rovnice tlaku jako funkce φ. Z extrému funkce p=f(φ) lze určit minimální, maximální tlak a tlakový poměr během jedné otáčky φ<0; 2π):

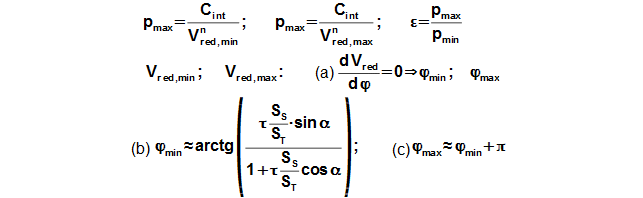
7.442 Maximální a minimální tlak a tlakový poměr.

ε [-] tlakový poměr; φ_min [rad] pootočení hřídele, při kterém bude redukovaný objem minimální V_red,min; φ_max [rad] pootočení hřídele, při kterém bude redukovaný objem maximální V_red,max. Pokud je zadáno p_max lze vypočítat integrační konstantu C_int z rovnice pro p_max. Úhly φ_min; φ_max lze určit iteračním výpočtem z Rovnice (a) a v prvním kroku iterace použít hodnoty z Rovnice (b) a (c) (φ_min; φ_max pro případ sinusového pohybu pístů). Odvození těchto rovnic je v Příloze 442.

Střední tlak oběhu se vypočítá podle věty o střední hodnotě funkce z funkce p(φ):

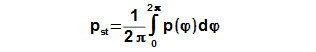8.443 Střední tlak oběhu.

Jestliže je zadán pouze střední tlak oběhu určí se C_int iteračním způsobem z výsledku Rovnice 8.

Stejným postupem lze odvodit rovnice pohybu pístů i pro ostatní modifikace Stirlingova motoru.

Stirlingův motor α-modifikace plněný héliem s klikovým mechanismem a těmito rozměry: průměr válce 68 mm (na teplé i studené straně je stejný průměr), poloměr kliky 22 mm, délka ojnice 105 mm, mrtvý objem na teplé straně 110 cm³, mrtvý objem na studené straně 90 cm³, objem regenerátoru 68,682 cm³, střední teplota plynu na teplé straně regenerátoru 900 K, střední teplota plynu na studené straně regenerátoru 330 K, střední tlak 15 MPa, úhlové zpoždění pohybu pístu na studené straně za pohybem pístem na teplé straně je 105°. Stanovte průběh tlaku v závislosti na pootočení hřídele a další důležité úhly oběhu.
Úloha 1.444

Úloha 1: průběh tlaku v motoru.

Změna teploty pracovního plynu ve Stirlingově motoru

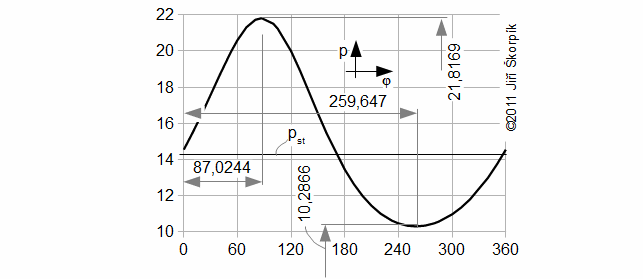
Pokud n≠1 znamená to mimo jiné, že se musí měnit i teplota pracovního plynu v jednotlivých objemech motoru podle rovnic:

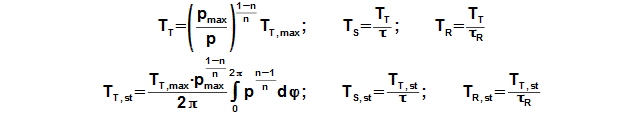
9.251 Teplota pracovního plynu v jednotlivých objemech motoru.

T_T [K] teplota pracovního plynu na teplé straně motoru; T_S [K] teplota pracovního plynu na studené straně motoru; T_R [K] teplota pracovního plynu v regenerátoru. Odvození bylo provedeno pro zjednodušující předpoklad T_TR=T_T; T_SR=T_S; index st označuje střední hodnotu teploty pracovního plynu za celý oběh. Odvození rovnic je v Příloze 251. Tato rovnice byla poprvé zveřejněna v [6].

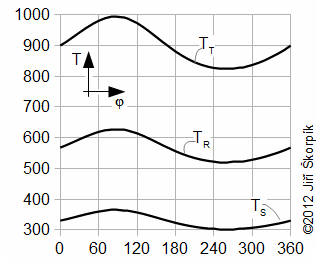
Jak je patrné z rovnic změna teploty kopíruje změny tlaku a je tím větší čím větší je střední teplota pracovního plynu ve vyšetřovaném objemu. Jestliže jsou zadány pro výpočet pouze střední hodnoty teplot (T_T,st; T_S,st; T_R,st), potom při výpočtu průběhu teplot se postupuje iteračním způsobem pro zjištění teploty T_T,max. To znamená, že v prvním kroku se teplota T_T,max odhadne, vypočítá podle Rovnice 11 teplota T_T,st a pokud se výrazně liší od zadané hodnoty výpočet opakovat s novým odhadem teploty T_T,max.

Vypočítejte průběh teploty pracovního plynu během jednoho pootočení hřídele (jeden oběh) na teplé a studené straně a v regenerátoru Stirlingova motoru o parametrech uvedených v Úloze 1.
Úloha 2.819

Úloha 2: souhrn zadání a výsledků.

Stirlingův oběh a Schmidtův oběh

Stirlingův oběh a Schmidtův oběh* jsou zjednodušené avšak velmi populární teoretické oběhy Stirlingových motorů, při kterých se zavádí předpoklad n=1. Stirlingův oběh předpokládá lineární pohyb pístů, Schmidtův oběh sinusový pohyb pístů. Podrobnosti o obou obězích například [4], [3].

Gustav Schmidt; 1826-1881: Profesor na Německém polytechnickém ústavu království Českého. Svůj oběh Stirlingova motoru publikoval v roce 1871.

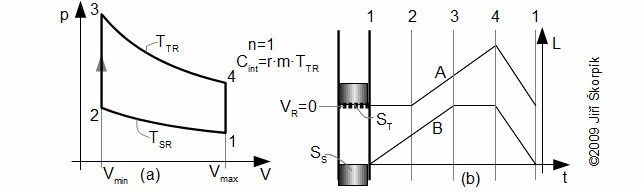
10.447 Stirlingův oběh.

(a) p-V diagram; (b) trajektorie pístů. r [J·kg^-1·K^-1] individuální plynová konstanta; m [kg] hmotnost pracovního plynu v pracovním objemu; t [s] čas. A trajektorie pístu na teplé straně; B trajektorie pístu na studené straně. Odvození rovnice je uvedeno v Příloze 447.

Další porovnávací oběhy Stirlingova motoru

Theodor Finkelstein definoval oběh pro n=κ, který modeloval metodou konečných prvků [3], [2, s. 87]. V současnosti nejpoužívanějším je oběh s adiabatickými změnami ve válcích a izotermickými změnami v mrtvých objemech motoru. Autory tohoto oběhu jsou Israel Urieli a David Berchowitz [1] (k řešení autoři sestavili soustavu diferenciálních rovnic, které řešili metodou Runge – Kutta). Soustava rovnic je popsána např. [4, s. 23 (strana ve vázané verzi práce)].

Pár slov na závěr

Zde popsaný termodynamický oběh vychází ze středních hodnot mnoha veličin, které jsou ve skutečnosti proměnné (teplotní poměry, index polytropy, který je pro každý objem jiný a pod). Hmotnost pracovního plynu v pracovním objemu motoru není také ve skutečnosti konstantní (střídavý vnik/únik pracovního plynu přes pístní kroužky viz článek 36. Ztráty ve Stirlingovýh motorech). Tyto okolnosti (především poslední zmíněná) podstatným způsobem ovlivňují tvary diagramů s čímž je potřeba počítat.

Odkazy

1. URIELI, Israel, BERCHOWITZ, David. Stirling Cycle Engine Analysis, 1984. 1. vydání. Bristol: Adam Hilger Ltd., ISBN 978-0996002196.

2. MARTINI, William. Stirling engine design manual, 2004. Přetisk vydání z roku 1983. Honolulu: University press of the Pacific, ISBN: 1-4102-1604-7.

3. WALKER, Graham. Dvigateli Stirlinga/Двигатели Стирлинга, 1985. Doplněný Ruský překlad knihy: WALKER, Graham Stirling engine, 1980. Oxford: Oxford University Press.

4. ŠKORPÍK, Jiří. Příspěvek k návrhu Stirlingova motoru, VUT v Brně, Edice PhD Thesis, 2008, ISBN 978-80-214-3763-0.

5. ŠKORPÍK, Jiří. A new comparative cycle of a Stirling engine, The 14th International Stirling Engine Conference, in Groningen – Netherlands, 2009, ISBN: 978-88-8326-022-3.

6. ŠKORPÍK, Jiří. Stirling engine cycle-supplement, The 15th International Stirling Engine Conference, in Dubrovnik-Croatia, 2012, ISBN: 978-88-8326-019-3.

Bibliografická citace článku

ŠKORPÍK, Jiří. Oběh Stirlingova motoru, Transformační technologie, 2009-07, [last updated 2012-01]. Brno: Jiří Škorpík, [on-line] pokračující zdroj, ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/34.html. English version: Stirling engine cycle. Web: https://www.transformacni-technologie.cz/en_34.html.