ZÁKLADNÍ ROVNICE KLIKOVÉHO MECHANISMU PARNÍHO MOTORU
www.transformacni-technologie.cz; Copyright©Jiří Škorpík, 2011-2020. All rights reserved. Tato publikace neprošla redakční ani jazykovou úpravou.
Úvod
Pro dimenzování hlavních částí pístového parního motoru a jeho klikového mechanismu je nezbytné stanovit, rovnici polohy pístu, síly působící na píst, kroutící moment na hřídeli a rovnoměrnost chodu takového mechanismu.
Podkladem pro výpočet je konstrukce pístové skupiny motoru a tlaky pod a nad pístem, respektive jeho p-V diagram.
Klikový mechanismus převádí přímočarý vratný pohyb pístu na pohyb rotační a obráceně. Mechnaismus obsahuje píst s pístní tyčí, ojnici, kliku a hřídel, viz Obrázek 555.
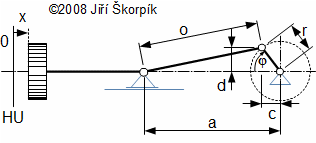558 Kinematická vazba pístu a klikového mechanismux [m] poloha pístu v závislosti na pootočení hřídele – aktuální vzdálenost pístu od jeho horní úvrati; o [m] délka ojnice pístu; r [m] rameno kliky; φ [°] pootočení hřídele.
Poloha pístu jako funkce pootočení hřídele
První rovnicí, kterou je potřeba sestavit je rovnice pro určení polohy pístu, kterou lze uvést jako funkce času nebo praktičtěji jako funkci úhlu pootočení hřídele, viz Rovnice 559. Úhel pootočení hřídele je ale sám funkcí času – tuto funkci lze odvodit z otáček hřídele.
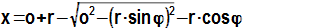
559 Rovnice polohy pístu spojeného s klikovým mechanismem
Odvození rovnic je uvedeno v Příloze 559, s. 9.
Síly působící na klikový mechanismus
Na píst, respektive mechanismus zajišťující pohyb pístu, působí síly od tlaku páry a setrvačné síly, jak ukazuje Obrázek 346. Tyto síly musí být vhodně zachyceny konstrukcí mechanismu.
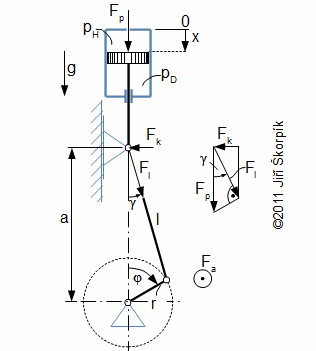346 Znázornění sil působící na klikový mechanismus jako funkce pootočení hřídele φpH [Pa] tlak páry na pístem; pD [Pa] tlak páry pod pístem; Fp [N] výsledná síla působící na klikový mechanismus ve směru posuvu pístu; Fk [N] síla působící na vodítko pístní tyče; Fa [N] sílá působíc na mechanismus v axiálním směru (ve směru osy hřídele); Fl [N] síla působící na ojnici; g [m·s-2] gravitační zrychlení. Modrá barva označuje vazby, které zachytávají síly.
● Výpočet sil působících na klikový mechanismus
Z posledního obrázku lze odvodit rovnice silové rovnováhy klikového mechanismu, přitom Vzorce 347 popisují síly působící na mechnismus ve směru posuvu pístu a Vzorce 764 popisují síly působící na mechanismus kolmo na směr posuvu pístu (z pohledu Obrázku 346 se jedná o sílu působící na vodítko pístní tyče). Axiální síla Fa by u ideálního klikového mechanismu neměla vznikat, ale vzniká v důsledku nesouososti čepů mechanismu – při běžné přesnosti výroby a seřízení je tato síla o řád až dva menší než síly ve dvou hlavních směrech.
síla Fa by u ideálního klikového mechanismu neměla vznikat, ale vzniká v důsledku nesouososti čepů mechanismu – při běžné přesnosti výroby a seřízení je tato síla o řád až dva menší než síly ve dvou hlavních směrech.
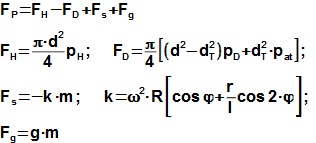
347 Rovnice pro výpočet sil působící na klikový mechanismus ve směru posuvu pístu
FH [N] výsledná síla působící na píst od tlaku páry v horní komoře; FD [N] výsledná síla působící na píst od tlaku páry v dolní komoře; Fs [N] setrvačná síla posuvných hmot, které jsou v propojeny mechanicky s pohybem pístu (smykadlo, pístní tyč, ojnice...); Fg [N] výslednice tíhových síly působicí na mechnismus (hmotnost pístu, pístní tyče, ojnice, hmotnost plynu...); d [m] průměr válce; pat [Pa] tlak atmosférický (skříň zalomené hřídele); dT [m] průměr pístní tyče; k [m·s-2] zrychlení posuvných hmot mechanismu (rovnice při zanedbání, některých nevýznamných členů, plný tvar rovnice je v příloze); m [kg] hmotnost posuvných hmot (v případě výpočtu tíhy se započítává hmotnsot celého mechanismu; v případě výpočtu setrvačných sil se počítají jen hmoty, které se posuvají ve směru posuvu pístu – ojnice nekoná posuvný pohyb, ale pohyb kombinovaný, proto se do setrvačných posuvných hmot zahrnuje pouze 1/3 hmotnosti ojnice); ω [rad·s-1] úhlová rychlost otáčení hřídele. Rovnice sil působící na píst jsou odvozena v Příloze 347, s. 8.
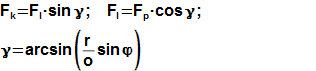
764 Rovnice pro výpočet sil působící kolmo na směr posuvu pístu (na vedení pístní tyče)
Fl [N] síla působící v ojnici; γ [°] úhel, který svírá ojnice se směrem pohybu pístu. Pro malé úhly γ cca do 20° je cos γ větší jak 0,9 a síla Fl je téměř totožná se sílou Fp. Odvození rovnic pro síly působící na vedení pístní tyče jsou uvedeny v Příloze 764, s. 9.
Obecně platí, že se zvyšujícími se otáčkami roste vliv setrvačných sil a klesá vliv sil od tlaku páry. Pro vyšetření setrvačných sil je musíme znát úhlovou rychlost otáčení hřídele. Obvykle se uvažuje jako konstantní, ale ve skutečnosti se mění, viz kapitola Nerovnoměrnost chodu klikového mechanismu, s. 6. Pokud je nerovnoměrnost chodu velká je nutné změny úhlové rychlosti započítat.
vliv sil od tlaku páry. Pro vyšetření setrvačných sil je musíme znát úhlovou rychlost otáčení hřídele. Obvykle se uvažuje jako konstantní, ale ve skutečnosti se mění, viz kapitola Nerovnoměrnost chodu klikového mechanismu, s. 6. Pokud je nerovnoměrnost chodu velká je nutné změny úhlové rychlosti započítat.
Výpočet těchto sil slouží ke stanovení namáhaní jednotlivých částí mechanismu, dimenzování ložisek apod. Při výpočtu těchto sil se vychází z navrženého nebo naměřeného p-V diagramu motoru, tyto diagramy se z praktických důvodů uvádí v procentech objemu p-V[%], respektive v procentech okamžité polohy pístu p-x[%]. Pro takový případ je nutný přepočet na odpovídající pootočení hřídele. Vzorce pro tento přepočet není složité odvodit za pomocí výše uvedených vzorců, viz Vzorec 768.
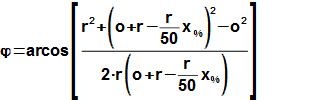
768 Přepočet polohy pístu vyjádřený v procentech na odpovídající hodnotu pootočení hřídele
Odvození této rovnice je uvedeno v Příloze 768, s. 11.
Odtud lze sestrojit graf závislosti jednotlivých sil na poloze pístu, ze kterého lze vycházet při pevnostních výpočtech motoru a zatěžování ložisek, viz Obrázek 766.
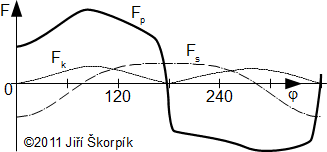
766 Průběh jednotlivých sil jako funkce pootočení hřídele
Jedná se o typický průběh jednotlivých sil pro otáčky 1 500 min-1.
● Zachytávání sil v klikovém mechanismu
Síly ve směru posuvu jsou zachytávané radiálními ložisky hřídele, síly kolmé na posuv pístu (včetně axiáních sil) zachytává vedení pístní tyče, axiální ložisko hřídele a píst – klikový mechnismus lze konstruovat i bez pístní tyče a ojnice je spojena přes čep přímo s pístem (to je možné například u jednočinných motorů podobně jako u spalovacích motorů). Vedení pístní tyče může být jednostranné i oboustranné (křižák, viz Obrázek 765b). U jednostranného vedení (Obrázek 765a) mohou být otáčky motoru pouze jedním směrem, a to takovým, aby výslednice sil působila vždy jedním směrem. Ale i v případě otáček pouze v jednom smyslu v některých případech (po započtení setrvačných sil a různých ztrát, které ovlivňují kroutící moment na hřídele) působí síla v jisté fázi otočení hřídele i v opačném směru. Tato síla bývá mnohem menší než síla působící kolmo na styčnou plochu smykadla. Proto každé vedení pístní tyče musí být opatřeno oboustranným vedením, viz Obrázek 765.
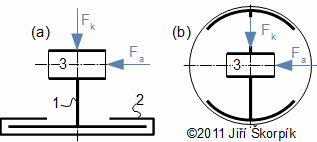
765 Základní způsoby vedení pístní tyče
(a) ploché vodítko; (b) válcové vodítko. 1 smykadlo; 2 vodící lišty; 3 otvor pro čep pístní tyče. Podrobné řešení např. [1].
Vedení pístní tyče klouže po smykadle, které má určitou plochu a je intenzivně mazáno, aby nedocházelo k velkému tření, což by vedlo k vysokým mechanickým ztrátám motoru a opotřebení.
V některých případech (především u pístové skupiny bez pístní tyče, kdy boční síly zachytává píst) bývá osa čepu ojnice posunuta od osy hřídele [4]. Tím lze zmírnit extrémy průběhu bočních sil – změní se samozřejmě i tvar Rovnic 347 a Rovnic 764 na s. 2.
síly zachytává píst) bývá osa čepu ojnice posunuta od osy hřídele [4]. Tím lze zmírnit extrémy průběhu bočních sil – změní se samozřejmě i tvar Rovnic 347 a Rovnic 764 na s. 2.
Vypočítejte síly Fp, Fs a Fk v důležitých okamžicích p-V diagramu. Jestliže máte k dispozici p-V diagram z Úlohy 573 uvedené v kapitole Vnitřní výkon pístového parního motoru, rozměry mechanismů včetně válce a jejich hmotnosti a otáčky hřídele. Vliv gravitačního zrychlení zanedbejte. Řešení úlohy je uvedeno v Příloze 767, s. 9.
Stejné nebo jen mírně upravené rovnice lze použít při vyšetřování sil působící na jakýkoliv klikový mechanismus, například šoupátka motoru, viz Úloha 769.
Vypočítejte síly působící na šoupátko Fp, Fs a Fk v důležitých okamžicích p-V diagramu Úlohy 573 uvedené v kapitole Vnitřní výkon pístového parního motoru. Jestliže máte k dispozici p-V diagram, rozměry mechanismů včetně šoupátka a jejich hmotnosti a otáčky hřídele. Vliv gravitačního zrychlení zanedbejte. Mechanismus šoupátka je popsán v článku Vyšetření pohybu a rozměrů šoupátka.
Kroutící moment a ztráty v klikovém mechanismu
Kroutící moment (jeho průběh v závislosti na pootočení hřídele) přenášený na hřídel motoru, respektive indikovaný na jeho výstupním konci je součtem momentů vznikající v klikovém mechanismu od několika sil. Těmito sílami je výslednice sil Fp působící na písty, které jsou propojené s hřídelí, setrvačné hmoty ostatních mechanismů, které jsou přes hřídel poháněny (pohon rozvodů páry, pohon regulace otáček a pod.) a energetické ztráty třením [2, s. 321] připojených mechanismů (tření v ložiscích, uložení pístní tyče, pístní kroužky o válec a pod.), viz Vzorec 773. Zjednodušujícím předpokladem této kapitoly je, že otáčky motoru jsou konstantní a není proto nutné počítat s kroutícím momentem vznikající v důsledku setrvačných sil rotujících částí motoru, viz následující kapitola.
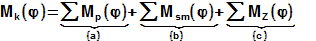
773 Kroutící moment na výstupním hřídeli motoru
Mk [N·m] kroutící moment na výstupním konci motoru; a [N·m] výsledný kroutící moment od jednotlivých pístů; b [N·m] výsledný krouticí moment od setrvačných sil dalších mechanismů propojených s hřídelí (například mechnaismus šoupátka, reg. mechanismi apod); c [N·m] výsledný kroutící moment způsobený třením v mechanismech propojených s hřídelí. Momenty působíc ve směru otáčení hřídele jsou kladné, momenty v opačném směru jsou záporné.
Jednotlivé momenty lze získat z rozkladu sil v klikovém mechanismu podle Obrázku 774.
Kroutící moment od sil vznikající při tření pohyblivých částí mechanismů se vypočítává podle typu ztrát. Hlavní třecí ztráty vznikají při přímočarém vratném pohybu (například pístní tyče o její ucpávky, tření vodítka o jeho vedení...) a v ložiscích, jak hlavních ložisek hřídele, tak v ložiscích ojnic, viz Obrázek 775.
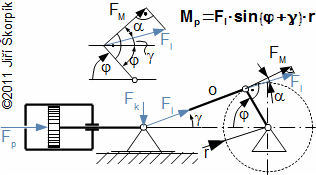
774 Výpočet kroutícího momentu od sil působící na píst
Stejným způsobem lze vypočítat kroutící moment od setrvačných hmot dalších mechanismů spojených s hřídelí jako je například pohon rozvodů páry parního motoru apod. Modře jsou označeny síly, které už byly počítány v předchozí kapitole. Odvození této rovnice je uvedeno v Příloze 774, s. 12.
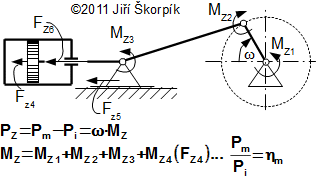
775 Vyznačení třecích sil a momentů v klikovém mechanismu a jejich vliv na přenášený výkon
MZ1 [N·m] třcí moment vznikající třením v hlavních ložiscích hřídele; MZ2 [N·m] třecí moment vznikající třením v ojničních ložiscích; MZ3 [N·m] třecí moment vznikající třením v ojničních čepech; FZ4 [N] třecí síla vznikající při tření pístních kroužků a pístu o válec; FZ5 [N] třecí síla vznikající tření vedení pístní tyče; FZ6 [N] třecí síla vznikající při tření pístní tyče o ucpávky. Pm [W] mechanický výkon klikového mechanismu na konci hřídele; Pi [W] vnitřní výkon motoru; Pt [W] třecí výkon mechanismu způsobený třecími ztrátami v klikovém mechanismu; ηm [-] mechanická účinnost klikového mechanismu.
Třecí síla FZ4 (tření ve válci)působí proti pohybu a na třecí kroutící moment se přepočítá stejným způsobem jako síla působící na píst uvedená v Rovnici 774.
Výpočet ztrátového momentu MZ se provádí ze stykových sil působící v ložisku a dalších kluzných plochách, olejové mezeře, vlastnosti maziva a kluzných ploch. Je zřejmé, že bude záviste i na pootočení hřídele, protože sledované síly se mění. Při základním návrhu klikového mechanismu, respektive stanovení výsledného kroutícího momentu Mk lze postupovat i obráceně a ztrátový moment vypočítat z odhadu mechanické účinnosti klikového mechanismu. Z něj lze alespoň přibližně stanovit střední hodnota ztrátového momentu.
mezeře, vlastnosti maziva a kluzných ploch. Je zřejmé, že bude záviste i na pootočení hřídele, protože sledované síly se mění. Při základním návrhu klikového mechanismu, respektive stanovení výsledného kroutícího momentu Mk lze postupovat i obráceně a ztrátový moment vypočítat z odhadu mechanické účinnosti klikového mechanismu. Z něj lze alespoň přibližně stanovit střední hodnota ztrátového momentu.
Odtud lze sestrojit graf závislosti jednotlivých momentů na poloze pístu, respektive pootočení hřídele jako na Obrázku 777, ze kterého lze vycházet při dimenzování klikového mechanismu.
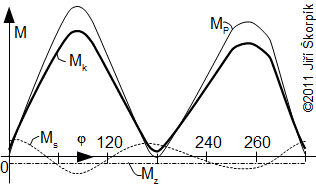
777 Průběh jednotlivých momentů jako funkce pootočení hřídele
φ [°]. Jedná se o klikový mechanismus jednoválcového dvojčinného parního motoru s jedním šoupátkem. Zde je ztrátový moment pro zjednodušení uváděn jako konstanta.
Vypočítejte kroutící moment na hřídeli klikového mechanismu. Rozměry mechanismů, síly působící na píst a šoupátko a setrvačné síly jsou stejné jako u Úlohy 767 a Úlohy 769. Předpokládejte mechanickou účinnost klikového mechanismu 90 %. Řešení úlohy je uvedeno v Příloze 776, s. 13.
Nerovnoměrnost chodu klikového mechanismu
Mechanický výkon na hřídeli motoru je odváděn ke spotřebiči mechanického výkonu, kterým nejčastěji el. generátor, ale může jim být i čerpadlo nebo jiný pracovní stroj. Zároveň musí platit energetická rovnováha mezi prací motoru a prací pracovního stroje. Práce vykonaná motorem za jednotku času je závislá na průběhu kroutícího momentu Mk během sledovaného časového úseku, mění se tedy v průběhu jedné otáčky motoru i předávaný výkon.
Příkon většiny typů pracovních strojů je funkcí otáček, respektive úhlové rychlosti a při změně výkonu motoru se musí změnit i úhlová rychlost soustrojí tzv. regulace pracovního stroje otáčkami. Úhlová rychlost soustrojí bude klesat nebo narůstat oproti střední úhlové rychlosti ω¯ podle toho, jaká bude okamžitá výkonová bilance mezi motorem a pracovním strojem. Poměr velikosti rozdílu mezi maximální a minimální úhlovou rychlostí ku střední úhlové rychlosti se nazývá nerovnoměrnost chodu [3, s. 35], viz Vzorec 783.
Předchozí kapitoly a úlohy pracovaly s odhadem otáček motoru n respektive odhadem střední úhové rychlosti ω¯. Pomocí této kapitoly lze ověřit jak moc se tento odhad bude lišit od skutečnosti. Dobře odhadnuté otáčky by se od těch vypočítaných odlišují jen nevýznamně. V opačném případě je nutné otáčky lépe odhadnout a celý návrh motoru až po tuto část provést znovu.
Velká změna úhlové rychlosti během otáčky může mít nepříznivý vliv na namáhání konstrukce soustrojí popřípadě práci pracovního stroje, například pro pohon čerpadel se doporučuje nerovnoměrnost chodu max kolem 1/20 pro pohon el. generátorů střídavého proudu až 1/300. Pro plynulost chodu je nutné zvětšit moment setrvačnosti hřídele soustrojí, respektive instalovat na hřídel motoru setrvačník, který zvýší moment setrvačnosti hřídele soustrojí, přenáší kliku přes mrtvé polohy, zmenší nerovnoměrnosti otáčení motoru v rámci jedné otáčky, při náhlém výpadku zatížení motoru se motor pomalejí roztočí (snížení požadavku na rychlost uzavření páry při výpadku zatížení) popřípadě strvačník pomáhá překonávat náhle velké odpory (lis apod.).
pro pohon el. generátorů střídavého proudu až 1/300. Pro plynulost chodu je nutné zvětšit moment setrvačnosti hřídele soustrojí, respektive instalovat na hřídel motoru setrvačník, který zvýší moment setrvačnosti hřídele soustrojí, přenáší kliku přes mrtvé polohy, zmenší nerovnoměrnosti otáčení motoru v rámci jedné otáčky, při náhlém výpadku zatížení motoru se motor pomalejí roztočí (snížení požadavku na rychlost uzavření páry při výpadku zatížení) popřípadě strvačník pomáhá překonávat náhle velké odpory (lis apod.).
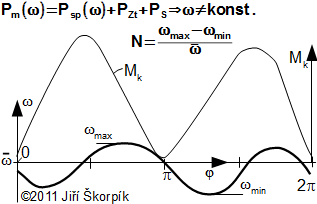
783 Jestliže příkon pracovního stroje je funkcí úhlové rychlosti, bude se během otáčky motoru měnit i úhlová rychlost hřídele soustrojí
Psp [W] užitečný příkon pracovního stroje; PS [W] výkon rotačních hmot (změna kinetické energie rotačních hmot za jednotku času – při ω=konst. je PS=0 W ); PZt [W] ztráty mimo motor (ztráty ve spojce, generátoru...); ω¯ [rad·s-1] střední úhlová rychlost, při kterém střední kroutící moment motoru Mk,r vykoná během jedné otáčky motoru stejné množství práce Em jako při skutečné proměnlivé úhlové rychlosti vykoná kroutící moment Mk; n [s-1] otáčky motoru; N [-] nerovnoměrnost chodu; φ [rad].
● Součinnost setrvačníku a soustrojí
Velikost setrvačníku, respektive jeho momentu setrvačnosti [2, s. 258] se vypočítá z požadované nerovnoměrnosti chodu. Obvykle se postupuje iteračně tak, že se nejdříve odhadne moment setrvačnosti rotačních hmot a odtud vypočítá průběh úhlové rychlosti během jedné otáčky ze známého průběhu kroutícího momentu a konkrétní výkonové charakteristiky pracovního stroje. Následně se vypočítá nerovnoměrnost chodu. Pokud nerovnoměrnost chodu není v požadovaném rozsahu výpočet se opakuje pro korigovaný moment setrvačnosti setrvačných hmot.
kroutícího momentu a konkrétní výkonové charakteristiky pracovního stroje. Následně se vypočítá nerovnoměrnost chodu. Pokud nerovnoměrnost chodu není v požadovaném rozsahu výpočet se opakuje pro korigovaný moment setrvačnosti setrvačných hmot.
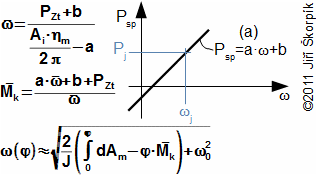
784 Příklad rovnic pro výpočet úhlové rychlosti pro případ lineární příkonové charakteristiky spotřebiče (asynchronní generátor)
(a) charakteristika spotřebiče (asynchronní generátor). Pj [W] jmenovitý výkon el. generátoru; ωj [rad·s-1] jmenovitá úhlová rychlost el. generátoru; J [kg·m2] moment setrvačnosti hřídele soustrojí (včetně setrvačníku); Am [J] indikovaná práce na výstupním konci hřídele motoru; ω0 [rad; °] úhlová rychlost hřídele při φ=0°. Při odvozování těchto rovnic byly použity různé zjednodušující předpoklady, které omezují jejich platnost pouze na nízké hodnoty rovnoměrnosti chodu N. Uvedené rovnice jsou tím přesnější, čím menší je nerovnoměrnost chodu. Odvození této rovnice je uvedeno v Příloze 784, s. 14.
Vypočítejte potřebný moment setrvačnosti rotoru soustrojí, jestliže znáte kroutící moment na výstupní hřídeli motoru i moment setrvačnosti hřídele soustrojí. Jedná se o motor jako v předchozích úlohách. Motor pohání asynchronní el. generátor, jehož jmenovitý výkon je 15 kW, jmenovité otáčky 1 545 min-1 a nulového výkonu dosahuje při otáčkách 1 500 min-1. Ztrátový výkon generátoru je 1 500 W. Požadovaná rovnoměrnost chodu je 1/300. Řešení úlohy je uvedeno v Příloze 785, s. 16.