Úvod
Fotony jsou částice, které přenáší energii. Nejblíže je lidským smyslům proud fotonů ve formě světelného paprsků. V tomto případě vznikájí fotony ve zdroji světla (Slunce, plamen apod), ale existují i jiné zdroje – například i rádiové, televizní i Wi-fi signály nejsou ničím jiným než proudem fotonů.
U fotonu se velmi výrazně projevují kvantové vlastnosti částic tj pohyb z místa vyzáření do místa dopadu má nejblíže k představě skoku, kdy nelze stanovit trasu skoku ale pouze pravděpodobnost dopadu do určitého místa. V místě dopadu foton zanikne předáním své energie a hybnosti částici, která ho pohltí.
Každé těleso vyzařuje elektromagnetické záření (fotony) odpovídající jeho teplotě. Kdyby nepřijímalo fotony z okolí tak, by postupně vychladlo. https://t.co/61MqGHMJ3F
— Jiří Škorpík (@jiri_skorpik) April 23, 2024
Odhad pravděpodobné trasy fotonu
Jestliže bychom znali okamžitý pohybový stav fotonu (jeho polohu a další parametry souvisejícím z jeho pohybem), pak by bylo možné stanovit pravděpodobnost jeho následujícího výskytu pro určité vzdálenější místo. K tomu musíme znát všechny možné trasy, po kterých se do onoho vyšetřovaného místa může dostat, a pro jednotlivé trasy znát i tzv. amplitudy pravděpodobnosti, které se sečtou, a tím dají výslednou pravděpodobnost, že foton do vyšetřovaného místa dorazí:
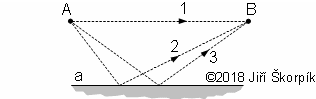 |
1.1180 Možné trasy fotonu. Foton o známem pohybovém stavu se z místa A do místa B může dostat několika možnými trasami. Těchto tras je obrovské množství, ale pro názornost jsou zde pouze tři. 1 přímá trasa; 2 trasa s odrazem s různými úhly dopadu a odrazu; 3 trasa s odrazem se stejným úhlem dopadu a odrazu. |
Amplituda pravděpodobnosti se po trase periodicky mění jako funkce sinus, ale současně se jedná o vektor přičemž směr amplitudy pravděpodobnosti je dán jejím úhlem, který se také periodicky opakuje v rámci vlnové délky a může mít tedy unikátní hodnotu 0 až 2π(1), respektive 0° až 360° (jedná se o sinusový vektor popsaný v kapitole Goniometrické a cyklometrické funkce). Výsledná amplituda pravděpodobnosti záleží na délce možné trasy fotonu, respektive na tom, kolikrát se průběh amplitudy pravděpodobnosti zopakuje:
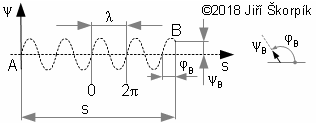 |
2.1181 Amplituda pravděpodobnosti možné trasy. ψ [-] amplituda pravděpodobnosti (ψB amplituda pravděpodobnosti pro bod B); λ [m] vlnová délka amplitudy pravděpodobnosti fotonu (dále jen fotonu); s [m] vzdálenost vyšetřovaného bodu B od počátku. |
Proč rozdělení vlnové délky na stupnici 0 – 2π, a ne třeba na 1-12? S radiánovou stupnicí se v tomto případě prostě lépe počítá, o tom píšu v kapitole Goniometrické a cyklometrické funkce s radiánovou stupnicí se lépe počítá.