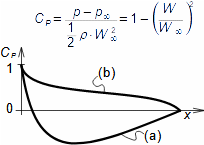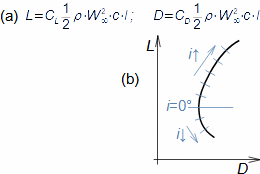Úvod
Aerodynamika
Profil
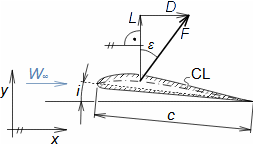
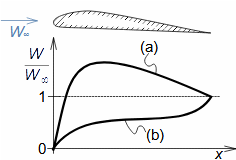
Aerodynamika vyšetřuje silové účinky proudění na obtékaná tělesa nebo kanál, ve kterém se nachází. Aerodynamika profilu je speciální oblast aerodynamiky, která zkoumá 2D obtékání těles, které mají proměnné rozměry pouze ve dvou směrech – jedná se o profilovanou desku, viz Obrázek 1. Profilem je nazýván řez tímto tělesem. Popis geometrie profilů a pravidel pro jejich kreslení je uveden například v článku Geometrie a materiály lopatkových strojů [Škorpík, 2009].
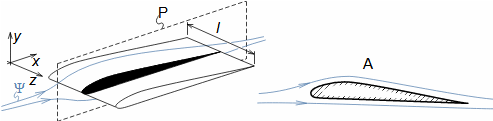
P rovina řezu; Ψ proudnice ve vyšetřované rovině; A znázornění vyšetřovaného profilu. l [m] délka profilové desky; x, y, z [m] souřadnice.
Nestlačitelné proudění
Při nízkých rychlostech se plyn chová podobně jako kapalina, která je nestlačitelná, ale s rostoucí rychlostí se začíná projevovat vliv nízké rychlosti zvuku plynech, které jsou v kapalinách mnohem vyšší. Rychlost zvuku je totiž rychlostí šíření tlakových poruch v tekutině. Navíc při nadzvukových rychlostech proudění může docházet k jevům souvisejících se skokovými změnami stavových veličin plynu, ke kterým při nižších rychlostech nedochází. Nicméně stlačitelnost plynu se na proudění významně projevuje až od rychlosti cca 0,3 Mach [Kadrnožka, 1991, s. 27]. Z toho důvodu je v tomto článku popsána teorie proudění nestlačitelného proudění a teorie stlačitelného proudění v článku Machovo číslo a efekty při proudění vysokými rychlostmi [Škorpík, 2021]).
Odpor profilu
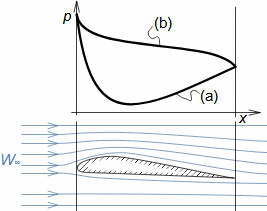
Při obtékaní jakéhokoliv tělesa proudem tekutiny působí tato tekutina na těleso silou. Tato síla vzniká kvůli změně hybnosti tekutiny v důsledku vloženého tělesa, změny tlaku v okolí tělesa a tření tekutiny o plochu tělesa. Složka síla ve směru nátokové rychlosti (směr volného proudu před tělesem) se nazývá odpor.
Třecí odpor
Tvarový odpor
Odpor vzniká třením tekutiny o jeho povrch a případně dalšími efekty, které způsobují tlakovou diferenci mezi protilehlými stranami profilu. Příspěvek od třecích sil se nazývá zkráceně třecí odpor, a od tlakových tlakový odpor nebo tvarový odpor, který vzniká vždy, protože tlakové diference Δp mezi čelní a zádní plochou profilu vzniknou i při proudění bez tření. Výsledný odpor profilu je jen přibližně součtem obou dvou odporů, viz Rovnice 2(a), protože se vzájemně ovlivňují.