ENERGY BALANCES OF TURBOMACHINES

Jiří Škorpík, ORCID: 0000-0002-3034-1696, skorpik.jiri@email.cz
Introduction
Energy balance of water turbine
Energy balance of pump
Discussion about pump energy equations
Energy balance of heat turbine
Adiabatic expansion inside heat turbine ● Polytropic expansion inside heat turbine
Energy balance of turbocompressor
Adiabatic compression inside compressor ● Polytropic compression inside compressor
Energy balance of fan
Energy balance of wind turbine
Propellers
References
Appendices – only in Czech language
This article in PDF
The article of online continued resource Transformační technologie; ISSN 1804-8293;
www.transformacni-technologie.cz; Copyright©Jiří Škorpík, 2006-2020. All rights reserved. This work was published without any linguistic and editorial revisions.
● 13. Energy balances of turbomachines ●

Introduction

Inside a turbomachine can be changed of enthalpy, kinetic energy and potential energy of a working gas according the equation for First law of thermodynamics for open system and it is can use for all types of turbomachines. In next chapters there is description of transformation energy for various types of the turbomachines (include losses), so as it is usually used under practice.

In chapter Internal power output/input of turbomachine Pi is defined specific internal work ai. Other internal parameter of machine is its internal efficiency(1) ηi, which defines an quality of transformation of energy inside machine through a comparation real specific internal work with ideal specific internal work of the machine. Difference between the real specific internal work and ideal specific internal work is called specific internal losses of system/machine z(2).

(1)Remark
For cases of hydraulic machines is usually used a term hydraulic efficiency for the internal efficiency, for cases heat machines is usually used a term thermodynamic efficiency and for cases wind turbines and propellers is omitted word "internal".
(2)Remark
The internal power and efficiency is not influenced by the internal losses only, but even a leakage of machine see chapter 17. Losses through leakage.

Energy balance of water turbine

The water turbines can transform potential, kinetic and pressure energy of a working liquid to work and heat-internal losses (increase of internal energy of water):

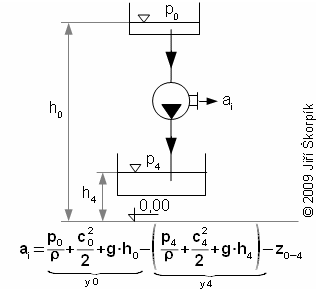Specific internal work of a water turbine. 1.303 Specific internal work of a water turbine.
ai [J·kg-1] specific internal work; p [Pa] pressure of working liquid; c [m·s-1] absolute velocity of flow; ρ [kg·m-3] density of working liquid; g [m·s-2] gravitational acceleration; h [m] height of levels; y [J·kg-1] specific total energy of working liquid; z [J·kg-1] specific internal losses. Derived from Bernoulli equation.
● 1 ●
● 13. Energy balances of turbomachines ●

An internal efficiency of the water turbine is ratio between ai and the change of specific total energy of the working liquid between the inlet flange and the exit flange:

Change of total energy of water in the turbine, hydraulic efficiency and a classification of losses.
2.596 Change of total energy of water in the turbine, hydraulic efficiency and a classification of losses.
Δy1-2 [J·kg-1] change of specific total energy of water in turbine; z1-2 [J·kg-1] specific internal losses in turbine; ηi [-] internal efficiency of turbine. The derivation of this equation is shown in the Appendix 596.

The water turbine are one of the most efficiency turbomachines with ηi up to 95 %.

The water turbine usually feeds an electric generator, which has adequate power on its contacts.

Discussion about water turbine energy equations

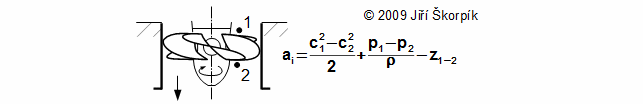
The change of specific energy inside an impeller of the water turbine.
3.305 The change of specific energy inside an impeller of the water turbine.
Work is done only inside the impeller of turbine and the change of specific energy of water inside the impeller is function of a difference of kinetic energy and pressure gradient (at negligible influence of the change of potential energy). Hence is advantageous used a reaction stage p1>p2, then is velocity less and therefore also the internal losses, which are function of the velocity.
● 2 ●
● 13. Energy balances of turbomachines ●

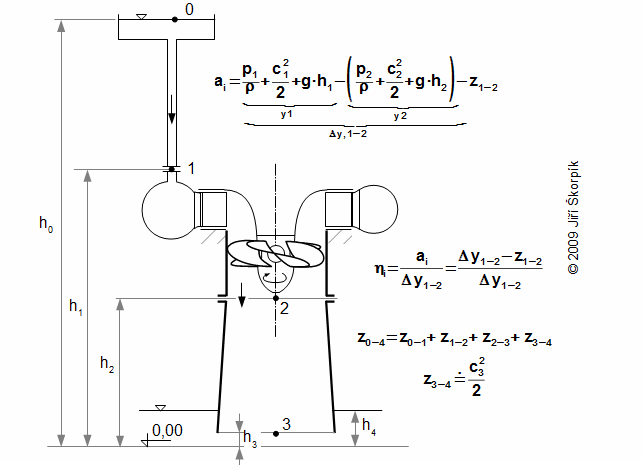
For technical reasons and safety of the water turbines are not placed tightly above the level of lower tank (a risk of flooding of machine room etc.). Hence, for case turbine with the reaction stage is inserted a draft tube between the turbine and the lower tank:

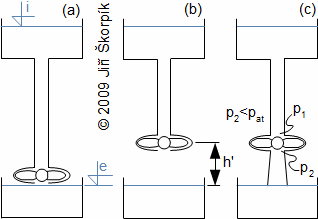
A description of function of the draft tube.
4.258 A description of function of the draft tube.
(a) the turbine is tightly above the level of the lower tank-maximum use of the potential difference h; (b) the turbine is higher than at previous case-the potential difference is less about the height h'; (c) using the draft tube is reduced pressure on the turbine exit, which is proportional to the water column h' (it allows use whole difference h).

The end of the draft tube is tightly below the surface of the lower tank and is filled water. Its height is function of difference of pressure between the turbine exit and the surface in lower tank. It evident, the pressure on the turbine exit must be less then the pressure on the surface of the lower tank. The pressure on the turbine exit p2 must not be less then saturation pressure of water in this point. In the opposite case the water column would be crashed under development of steam. Because pressure p2 is less than pressure p4 is the specific internal work of the turbine similar as for case a turbine without the draft tube, which is just above the surface of the lower tank. Through use of the draft tube can be used whole difference h.

Calculate the internal power output and the maximum length of a draft tube of a water turbine. Difference of the levels is 136 m, the flow rate 46 m3·s-1. Do not take into account any losses.The solution of this problem is shown in the Appendix 597.
Problem 1.597

Energy balance of pump

This case is similar such as the water turbines, but in rotodynamic pumps is transformed work (internal power input of the rotodynamic pump) to energy of the working liquid (potential, kinetic, pressure energy). The purpose of the pumps is to increase of specific total energy of the working liquid from a state y0 to required state y3:

● 3 ●
● 13. Energy balances of turbomachines ●
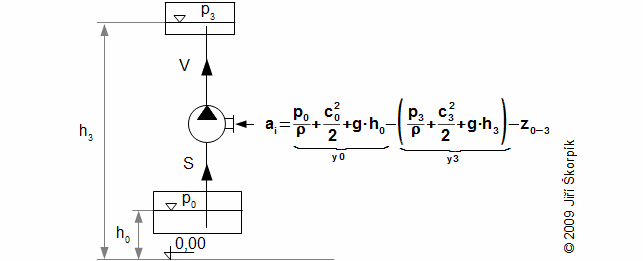
Change of total energy of liquid between the levels and the internal work of a pump.
5.300 Change of total energy of liquid between the levels and the internal work of a pump.
The letter S denotes the suction side of pump (here working liquid enters to the pump), the letter V denotes the delivery side of pump (here working liquid leaves from the pump). For the internal work of the pump is turth 0>ai.

Internal efficiency of the pump is ratio between the change of the total energy of the liquid during flow through the pump and the absolute value of internal work ai:

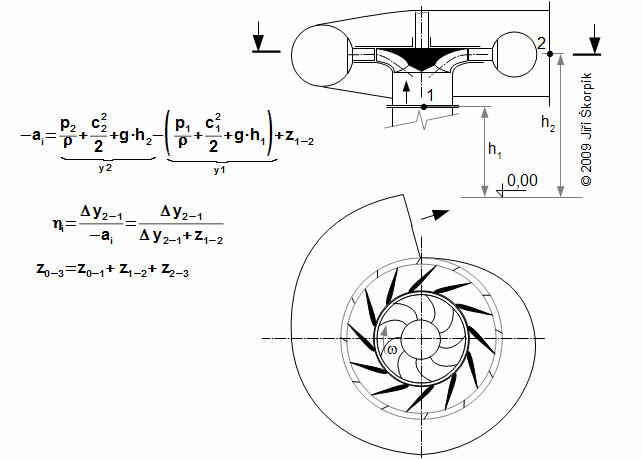
An increase of the specific total energy of the working liquid inside the pump, the internal efficiency and the classification of the internal losses.
6.599 An increase of the specific total energy of the working liquid inside the pump, the internal efficiency and the classification of the internal losses.

Maximum ηi of pumps can be higher then 90 %.

● 4 ●
● 13. Energy balances of turbomachines ●

Discussion about pump energy equations

During pumping of the working liquid can be neglected change of kinetic energy between the surface inside the suction and the delivery tank:

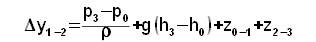A practical calculation of an increasing of the specific total energy of the working liquid inside the pump. 7.302 A practical calculation of an increasing of the specific total energy of the working liquid inside the pump.
The losses are calculated from a characteristic of piping system. The end of the tube is on a flanges of the pump. The derivation of this equation is shown in the Appendix 302.

Energy balance of heat turbine

Inside a heat turbine is transformed heat and ethalpy to work during expansion of the working gas. The working substance (liquid, gas, steam ...) is usually heated outside turbine, e.g. in case of steam turbines is made steam inside steam boiler (steam cycle), in case of a combustion turbine is made hot gas inside a combustion chamber in front of turbine (Brayton cycle).

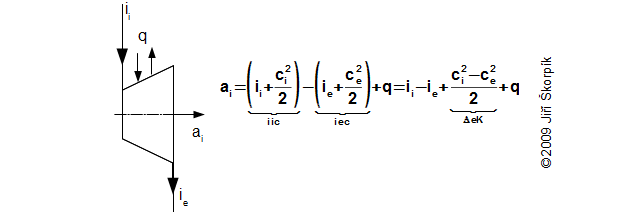
The specific internal work of the heat turbine.
8.306 The specific internal work of the heat turbine.
q [J·kg-1] specific heat of working gas transfer with surroundings; i [J·kg-1] specific enthalpy of working gas. Subscript i denotes inlet; e denotes exit; c stagnation state. ΔeK [J·kg-1] required change of kinetic energy between inlet and exit of machine (usually is required ΔeK≈0). The Derivation of this equation is from the general equation for internal work of the turbomachine at negligible change of potential energy.

The expansion of the working gas can be adiabaticaly(3) inside heat turbine, therefore q=0 nebo q≈0. There are cases where heat transfer with surroundings has influence on expansion (so called polytropic expansion q≠0). In two next chapters is descripted the cases adiabatic and polytropic expansion inside heat turbines.

(3)Remark
Inside the heat turbines is higher temperature of gas than is temperature of the surroundings, but are thermally isolated therefore heat transfer with surroundings is not actual.
● 5 ●
● 13. Energy balances of turbomachines ●

Adiabatic expansion inside heat turbine

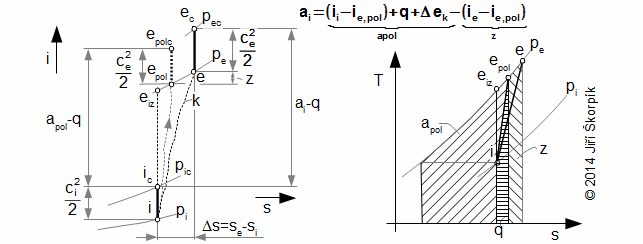
The working gas inside turbine expands from pressure pi on pressure pe. If the turbine is isolated system then entropy of working gas must be constant or increasing. This increase of entropy is caused by loss heat (local temperature differences, which arise during turbulence and a friction of the working gas on machine parts, flow of the working gas through leakages inside the stage and mixing etc.). For illustrate the heat flows inside the heat machine are used i-s diagram and T-s diagram:

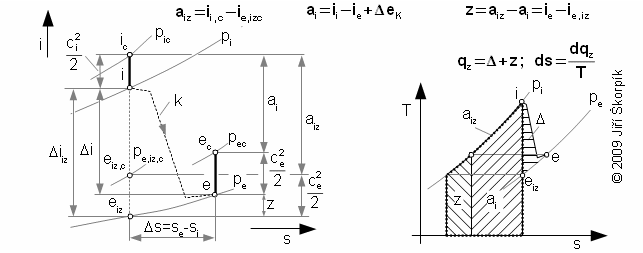
The specific internal work of the heat turbine at adiabatic expansion in i-s and T-s diagram.
9.307 The specific internal work of the heat turbine at adiabatic expansion in i-s and T-s diagram.
T [K] absolute temperature; aiz [J·kg-1] specific internal work at isentropic expansion (adiabatic expansion without losses); v [m3·kg-1] specific volume; Δiiz [J·kg-1] specific enthalpy difference at isentropic expansion; Δi [J·kg-1] used enthalpy difference; qz [J·kg-1] specific internal loss heat inside turbine; z [J·kg-1] specific internal losses inside turbine; Δ [J·kg-1] specific re-usable heat (part of qz, which was transformed on work in other part of turbine); k approximate profile of enthalpy change; s [J·kg-1·K-1] specific entropy. Derived for case q=0. How to design of T-s is described in the Appendix 307.

For the difference specific enthalpy ii-ie can be use the equation also:

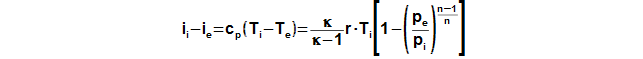
The difference of specific enthalpy between two states.
10.450 The difference of specific enthalpy between two states.
κ [-] Poisson index (heat capacity ratio); n polytropic index (for case flow without losses n=κ); r [J·kg-1·K-1] individual gas constant; cp [J·kg-1·K-1] specific heat capacity of working gas at constant pressure. Derived for cp=const. The derivation of this equation is shown in the Appendix 450.

From previous equations is evident, maximum ai at adiabatic expansion is reached for case isentropic process, therefore the isentropic expansion is used as comparative for assessment of internal efficiency of the heat turbine:

● 6 ●
● 13. Energy balances of turbomachines ●
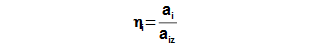The internal efficiency of the heat turbine in relation to isentropic process. 11.604 The internal efficiency of the heat turbine in relation to isentropic process.

Maximum ηi of heat turbines can be higher than 90 % (for case steam turbines 92% – for case multi-casing steam turbines, but the internal efficiency of individual turbine casings can be difference.

Calculate Pi of a steam turbine and the quality of the vapor on the exit turbine. Through the turbine flows 33 t·h-1 of steam, ηi=75 %, specific isentropic work of turbine is 1259,59 kJ·kg-1, exit pressure of turbine is 3 kPa, inlet pressure and temperature of turbine are 3,5 MPa, 450 °C.The solution of this problem is shown in the Appendix 871.
Problem 2.871

Polytropic expansion inside heat turbine

In cases heat transfer with surroundings influences expansion inside turbine. For example a cooling of temperature stressed of parts of the turbine etc. For these cases the expansion is more similar a polytropic expansion than adiabatic expansion.

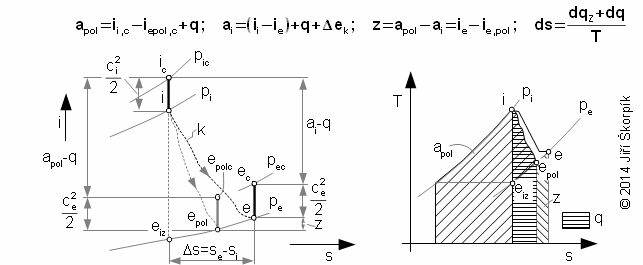
Internal work of turbine for case q>0.
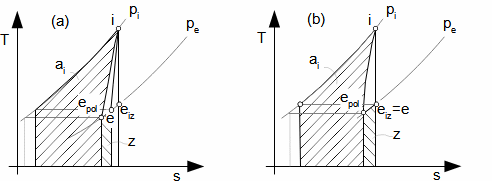
12.685 Internal work of turbine for case q>0.
eq state of working gas on the turbine exit for case heating of working gas at reversible polytropic expansion. apol [J·kg-1] specific internal work of reversible polytropic expansion(4) (expansion without losses) at heat q. The difference of specific kinetic energy of working gas are ignored here. How to design of T-s is described in the Appendix 685.
(4)Design of area in T-s diagram which is equivalent to work at expansion of gas
An equivalent area to heat q is subtracted from the area which equivalent to work apol, if it has negative sign and vice versa. An equivalent area to enthalpy change at constant pressure (ie-ie,q) is subtracted from the area apol if it has positive sign and vice versa.
● 7 ●
● 13. Energy balances of turbomachines ●
Internal work of turbine for case q<0.
13.686 Internal work of turbine for case q<0.
(a) the case: eiz>e; (b) the case: eiz=e (apparent isentropic expansion). A difference of kinetic energy of working gas are ignored here.

For case polytropic equations is maximum ai reached for case reversible polytropic expansion, therefore the reversible polytropic expansion is used as comparative for assessment of internal efficiency of heat turbine at polytropic expansion:

Internal efficiency of turbine in relation to reversible polytropic expansion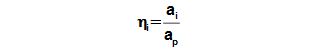. 14.908 Internal efficiency of turbine in relation to reversible polytropic expansion.
ap [J·kg-1] specific work at comparative (proposed) ideal polytropic expansion (usually isothermal expansion).

The above knowledge can be also applied to the description of expansion at heat transfer with surroundings in one stage of heat turbine.

Energy balance of turbocompressor

Inside the compressor is transformed work to the pressure energy of working gas.

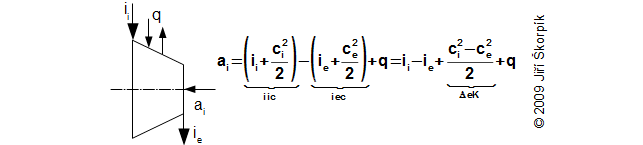
An specific internal work of the compressor.
15.117 An specific internal work of the compressor.
It is evident ai<0. The difference of kinetic energy on input and exit usually are negligible in relation the difference of enthalpy. The Derivation of this equation is from the general equation for internal work of the turbomachine at negligible change of potential energy.

The compression of the working gas can be presumed adiabaticaly inside compressor, therefore q=0 nebo q≈0. There are cases where heat transfer with surroundings has influence on the compression (so called polytropic compression q≠0). In two next chapters is descripted the cases adiabatic and polytropic compression inside heat compressors.

● 8 ●
● 13. Energy balances of turbomachines ●

Adiabatic compression inside compressor

The working gas is compressed from pressure pi on pressure pe inside the compressor. Also inside the turbocompressor arises the specific losses heat qz, which increase of the entropy as for case the turbine (see a description above the Equation 9):

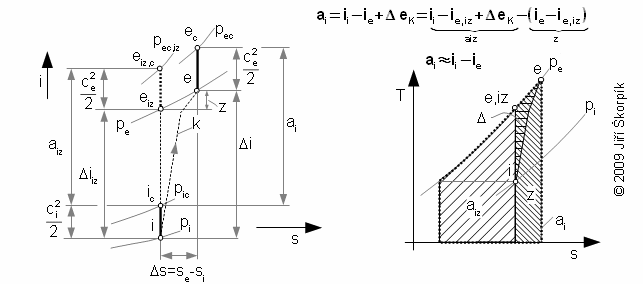
The specific internal work of the turbocompressor at adiabatic compression in i-s and T-s diagram.
16.118 The specific internal work of the turbocompressor at adiabatic compression in i-s and T-s diagram.
z [J·kg-1] specific internal losses (work that is necessary to deliver at compresion with losses, at reversible compression is z=0); Δ [J·kg-1] specific additional losses; k approximate compression curve.Design of T-s diagram is under static state of the working gas. The derivation of these equations is shown in the Appendix 118.

If is not known i-s diagram of the working gas, is can used for a calculation of enthalpy difference ii-ie also the Equation 10.

At adiabatic compression can be maximum ai reached for case isentropic compression, therefore the isentropic compression is used as comparative for assessment of the internal efficiency of the compressor at adiabatic compression:

Internal efficiency of the compressor at adiabatic compression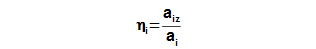. 17.609 Internal efficiency of the compressor at adiabatic compression.

A median of ηi is about 80 %, but for the best of constructions achieved 89 to 91 %.

A significant parameter of the compressors is also the compression ratio of compressor of the static or stagnation pressures:

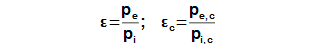The compression ratio of the compressor. 18.610 The compression ratio of the compressor.
ε [-] compression ratio.

The turbocompressor is driven by an electrical engine, by combustion turbine or turbo-expander. The turbocompressor is driven by a steam turbine in industrial plants with high consumption of pressurized air.

● 9 ●
● 13. Energy balances of turbomachines ●

Polytropic compression inside compressor

In cases heat transfer with surroundings influences compression inside compressors. For example a turbocompressor with cooling etc. For these cases the compression is more similar a polytropic compression than adiabatic compression.

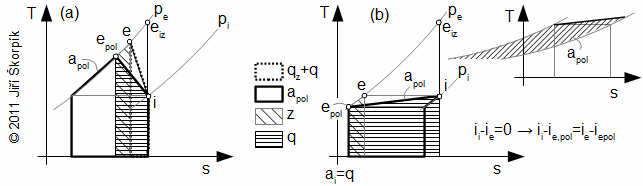
Internal work of compressor for case q>0.
19.687 Internal work of compressor for case q>0.(5)
eq state of working gas on exit of the turbocompressor for case heating of turbocompressor. A difference of kinetic energy of working gas is ignored here, see Appendix 687.
(5)Design of area in T-s diagram which is equivalent to work at compression of gas
The internal ideal polytropic work of compressor apol has negative sign, therefore for an image area, which equivalent to the internal work ai is true: the area, which equivalent to heat q is subtracted from the area apol if it has positive sign and vice versa. An equivalent area to an enthalpy change at constant pressure (ie-ie,q) is subtracted from the area apol if it has negative sign and vice versa.
Internal work of compressor for case q<0.
20.688 Internal work of compressor for case q<0.
(a) the case: z<-q; (b) the case: Te=Ti (apparent isentropic compression(6)). A difference of kinetic energy of working gas is ignore here.
(6)Remark
In this case, temperature of cooling fluid must be smaller than the temperature of working gas on input of the turbocompressor Ti.
● 10 ●
● 13. Energy balances of turbomachines ●

At polytropic compression can be maximum ai reached for case reversible polytropic compression, therefore the reversible polytropic compression is used as comparative for assessment of the internal efficiency of the compressor at polytropic compression:

Internal efficiency of compressor in relation to reversible polytropic compression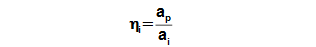. 21.1003 Internal efficiency of compressor in relation to reversible polytropic compression.
ap [J·kg-1] specific work at comparative (proposed) ideal polytropic compression (ap≠apol, because apol is influenced by losses at real compression see problem [26.612]).

The above knowledge can be also applied to the description of compression at heat transfer with surroundings in one stage of turbomachine.

Energy balance of fan

The fans are machines, which provide force of gas flow (compensate of pressure losses) with a small increase of its pressure. For calculation of the fans are usually used assumptions ρ≈const., t≈const.-incompressible flow. The work for the working gas is transformed on the pressure energy and the kinetic energy, a change of potential energy is negligible inside the fan. Because the compression ratio εc in the fan is very small is better to describe the transformation energy based on the increase stagnation pressure Δpc, then from equation of First law of thermodynamic for open system:

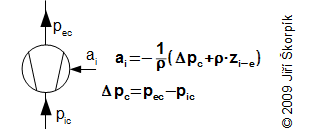Specific internal work of the fan shown in i-s digram. 22.309 Specific internal work of the fan shown in i-s digram.
Δpc [Pa] increase of stagnation pressure in fan. The assumption: potential energy is negligible. The derivation of this equation is shown in the Appendix 309.

The internal efficiency of the fan is defined as ratio between specific internal work of the fan without losses and the internal work of the fan:

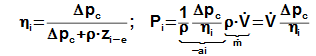Internal efficiency and power input of the fan. 23.581 Internal efficiency and power input of the fan.
V• [m3·s-1] volume flow; m˙ [kg·s-1] mass flow rate through fan.
● 11 ●
● 13. Energy balances of turbomachines ●

Energy balance of wind turbine

A portion of the kinetic energy, which flows through the rotor of the wind turbine is transformed to work (in case is negligible influence potential energy, internal heat energy and pressure energy). The flow area of the stream-tube of the wind rotor is increases under decreasing of the wind velocity inside. The slow-motion air flow of air behind the turbine is a barrier for surrounding flow (the flow on outside stream-tube), which must gradually wrap it. Therefore the stream-tube is developed (separated air flow, which flows through rotor from other air flow) far upstream of the turbine. Specific work of wind turbine is specific work of air inside stream-tube of rotor:

Transformation of energy through the wind turbine-axial stage.
24.311 Transformation of energy through the wind turbine-axial stage.
P.T. stream-tube of rotor. Derived from Bernoulli equation.

The axial wind turbine is a reaction stage. The stream-tube in front of turbine works as of a diffuser (pressure increasing) where the kinetic energy is transformed to pressure energy. The stream-tube behind turbine works as of a draft tube, because closely behind of turbine is developed a underpressure:

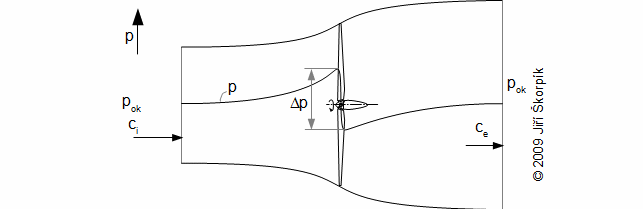
The profile of pressure inside the stream-tube of the wind axial rotor.
25.615 The profile of pressure inside the stream-tube of the wind axial rotor.
pok [Pa] pressure of air on input and exit of stream-tube of rotor; Δp [Pa] pressure difference of rotor.

Efficiency of wind turbine ηi is defined as the ratio between specific work ai and the specific optimum work of the wind turbine, which is reached if absolute velocity ce is one third of the absolute velocity ci:

● 12 ●
● 13. Energy balances of turbomachines ●
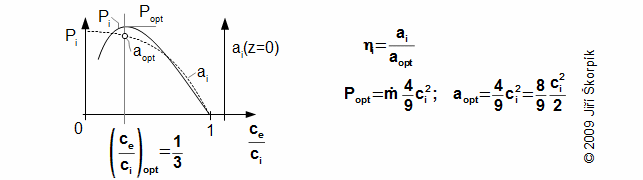
Specific optimum intrnal work of the wind turbine and its efficiency.
26.313 Specific optimum intrnal work of the wind turbine and its efficiency.
Popt [W] optimum power output of wind turbine; aopt [J·kg-1] specific optimum work of wind turbine; m• [kg·s-1] mass flow rate of air through rotor. The derivation of these equations are in the Appendix 313.

Propellers

The propellers, marine propellers are machines without a housing. The transformation energy by these machines is similar as for the case the wind turbines. The kinetic energy of the working fluid during flow through the rotor is increased-the velocity is increasing:

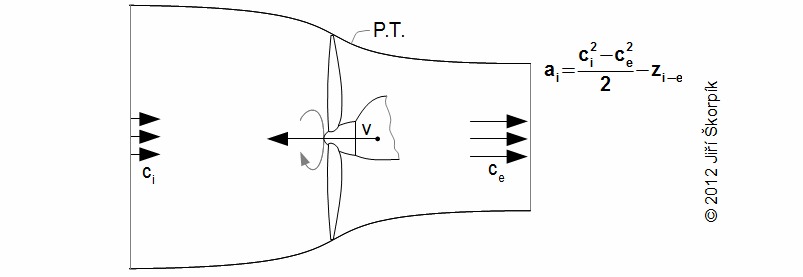
The transformation energy through the rotor of the propeller.
27.886 The transformation energy through the rotor of the propeller.
v [m·s-1] velocity of propeller in relation to frame of reference (word coordinate system), velocity ci and ce are in relation to this same frame of reference also. Derived from Bernoulli equation.

The propeller is used to make a thrust – a force, which causes a motion of an airplane or it is used for overcome the drag forces and weight forces during uniform flight. The most significant function of the propeller is to make the thrust:

● 13 ●
● 13. Energy balances of turbomachines ●
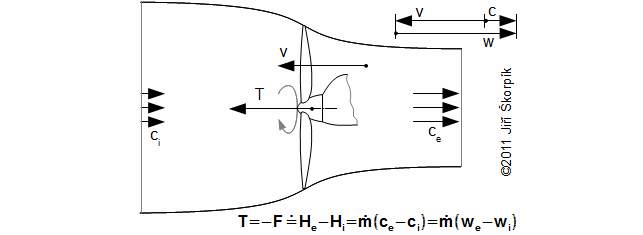
The thrust of the propeller drive.
28.177 The thrust of the propeller drive.
T [N] thrust of propeller drive (positive direction is at flight direction); F [N] force on control volume (stream-tube) from working fluid, which flows through control volume; w [m·s-1] relative velocity of working fluid. For the derivation of the equation of thrust of propeller was applied the Euler equation. The effect of pressure forces on input and exit of the stream tube are neutral, because they are the same. This equation is derived for case where the flight direction is parallel with flow (v // c). The influence the weight forces is negligible. Derivation of this equation is shown in [1].

The most significant quantity of the propeller drive is the thrust T, which allows the airplane an flight with velocity v, therefore the efficiency of the propeller is function these both quantities. The efficiency of the propeller shows qualitation of transformation of power input to the thrust. The efficiency transformation kinetic energy of realtive velocities of flow to the thrust is called propulsion efficiency:

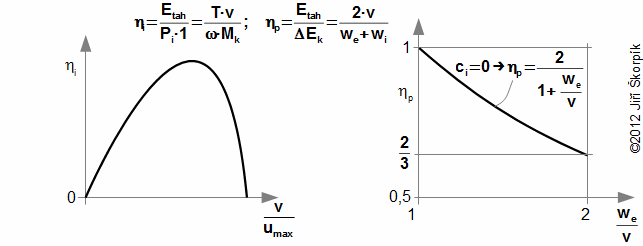
The propeller efficiency and propulsion efficiency of the propeller.
29.890 The propeller efficiency and propulsion efficiency of the propeller.
Etah [J·s-1] work of thrust per one second of flight; Pi·1 [J] work of drive of propeller per one second of flight; ω [rad·s-1] propeller speed; Mk [N·m] torque on shaft of the propeller; ηp [-] propulsion efficiency of propeller; ΔEK [J·s-1] change of kinetic energy inside stream-tube of propeller per one seconf of flight. The derivation of these equations are in the Appendix 890.

For optimal condition of the flight is efficiency of propeller ηi more than 90 % and efficiency ηprop circa 85 % [2, p. 613].

● 14 ●
● 13. Energy balances of turbomachines ●

References

1. Unified Propulsion, 2011. [Online] kurz v rámci projektu MIT OpenCourseWare Massachusetts Institute of Technology. Adresa: http://ocw.mit.edu.

2. MATTINGLY, Jack, HEISER, William, PRATT, David. Aircraft Engine Design, 2002. Second edition. Reston: American Institute of Aeronautics and Astronautics, ISBN 1-56347-538-3.

3. KADRNOŽKA, Jaroslav. Teorie lopatkových strojů, 1991. 3. vydání, přepracované. Brno: Vysoké učení technické v Brně, ISBN 80-214-0275-X.

4. KRBEK, Jaroslav. Tepelné turbíny a turbokompresory, 1990. 3. vydání. Brno: Vysoké učení technické v Brně, ISBN 80-214-0236-9.

Citation this article

This document is English version of the original in Czech language: ŠKORPÍK, Jiří. Energetické bilance lopatkových strojů, Transformační technologie, 2009-10, [last updated 2017-11-19]. Brno: Jiří Škorpík, [on-line] pokračující zdroj, ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/13.html. English version: Energy balances of turbomachines. Web: http://www.transformacni-technologie.cz\en_13.html.

● 15 ●