| Stirlingův motor |   |
Energetická bilance oběhu Stirlingova motoru umožňuje přibližně stanovit, pomocí indikátorového diagramu nebo vypočítaného průběhu tlaku ve Stirlingově motoru, teplo přivedené, odvedené, regenerované, vnitřní práci motoru a vnitřní tepelnou účinnost oběhu.
Postup, který je zde uveden je analytický prostřednictvím rovnic odvozených přímo z rovnic prvního zákona termodynamiky. Pomocí odvozených rovnic lze vypočítat základní energetické toky a jejich závislosti na dalších veličinách.
Tato energetická bilance platí za určitých ''zjednodušujících předpokladů'', které zjednodušují řešení. Vypočítané výsledky se tedy od skutečnosti liší v závislosti na tom, jak jsou skutečné děje vzdálenější od zjednodušujících předpokladů. Těmito zjednodušujícími předpoklady jsou: (1) Pracovní plyn je ideální plyn. – (2) Množství pracovního plynu v pracovním objemu motoru je konstantní. – (3) Nedochází k tlakovým ztrátám, tlak pracovního plynu je stejný v celém pracovním objemu. – (4) Regenerátor je dokonale tepelně izolován. – (5) Je známa závislost změny objemů na pootočení hřídele (respektive času) a změna tlaku na pootočení hřídele p(φ), VT(φ) a VS(φ). – (6) Oběh je ustálený.
Vnitřní práce motoru je dána tlakem a pracovním objemem motoru:
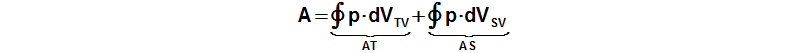
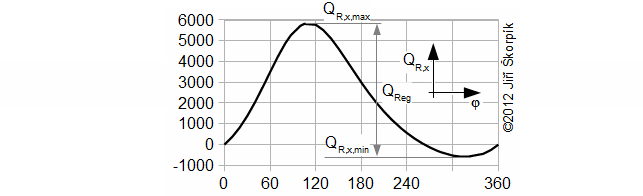
Ve Stirlingově motoru se transformuje teplo na práci. Pro tuto transformaci platí zákonitosti pro tepelný oběh, to znamená, že pouze část tepla přivedená do motoru se transformuje na práci a zbylou část je nutné z motoru odvést. K přívodu a odvodu tepla z motoru je potřeba teplotní gradient mezi pracovním plynem a teplosměnnými plochami motoru. Tento teplotní gradient se během jednoho oběhu mění, protože se mění teplota pravního plynu (viz kapitola Změna teploty pracovního plynu ve Stirlingově motoru), a proto probíhá v každé části motoru jak ohřev pracovního plynu tak jeho ochlazování. Přesto, jak lze usuzovat z principu motoru, tepelná bilance teplé strany motoru za jeden oběh bude kladná (teplo je zde pracovnímu plynu přivedeno), studené záporná (teplo je zde pracovnímu plynu odvedeno), tepelná bilance regenerátoru musí být nulová:
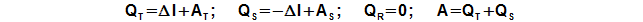
Teplo ΔI je do oběhu přivedené na teplé straně pro zvýšení vnitřní tepelné energie pracovního plynu a odvedené na straně studené (výsledná bilance za celý oběh). Toto teplo zatěžuje teplosměnné plochy a snižuje tepelnou účinnost oběhu. Na druhou stranu se jedná o teplo, které vytváří teplotní gradient mezi teplou a studenou stranou motoru i v případě, že mezi teplou a studenou stranou motoru je regenerátor s nízkou kapacitou nebo dokonce chybí. V případě izotermických termodynamických změn na teplé a studené straně motoru (například jak je předpokládá Schmidtova idealizace) je změna entalpie nulová.
Vnitřní práci motoru lze nepřímo měřit například indikací tlaku pracovního plynu v motoru nebo měřením práce na hřídeli (v tomto případě je nutné znát mechanické ztráty). Vnitřní práci lze přibližně vypočítat bez uvažování ztrát postupem uvedeným v článku Oběh Stirlingova motoru nebo s uvažovaním ztrát podle postupu uvedeného v článku Ztráty ve Stirlingových motorech.
Teplo QT a QS je možné určit z měření tepelného toku do/z motoru nebo přibližně vypočítat pomocí odhadu vnitřní tepelné účinnosti:
Vnitřní tepelná účinnost motoru je poměr práce A a tepla do motoru dodaného z vnějšku za jeden oběh QD*, respektive je definována jako účinnost tepelného oběhu, protože v motoru se realizuje celý oběh. Za podmínek uvedených v první kapitole lze stanovit vztahy mezi tepelnými toky:

Vnitřní tepelnou účinnost motoru lze odhadnout na základě podobnosti Stirlingových motorů podobné konstrukce:
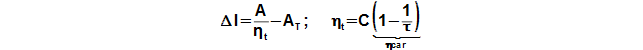
Regenerované teplo v regenerátoru je možné vypočítat z průběhu funkce, která popisuje sdělené množství tepla pracovnímu plynu v regenerátoru mezi počátkem oběhu a libovolným bodem oběhu. Regenerované teplo odpovídá rozdílu maximální a minimální hodnoty této funkce:
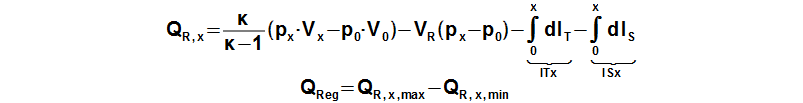
V případě izotermických dějů na teplé i studené straně motoru nedochází ke změně entalpie pracovního plynu na teplé a studené straně motoru, respektive v Rovnice 5 se dosadí IT,x=0; IT,x=0.
Teplo QReg lze analyticky přibližně vypočítat jestliže množství regenerovaného tepla QReg je mnohem více než tepla ΔI:
Při řešení poslední úlohy byl zanedbán vliv změny entalpie pracovního plynu na teplé a studené straně motoru, respektive tepla ΔI. Ve skutečnosti s klesajícím teplotním poměrem τ se vliv změny entalpie zvyšuje, respektive poměr mezi teplem QReg a teplem QD významně klesá a řešení použité v Úloze 3 zvyšuje svou nepřesnost. Tuto skutečnost je nutné brát v úvahu při dimenzování velikosti regenerátoru:
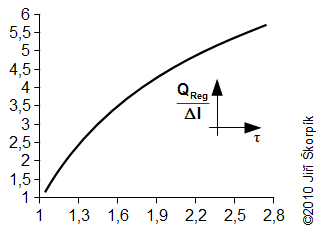 |
6.197 Poměr tepla QReg ku teplu ΔI v závislosti na teplotním poměru τ. Křivka zkonstruovaná z výledků Úlohy 2 a Úlohy 3. |
Rovnici pro změnu měrné entropie pracovního plynu v motoru vzhledem k počátku jednoho oběhu lze odvodit z rovnice pro První zákon termodynamiky pro uzavřený systém:
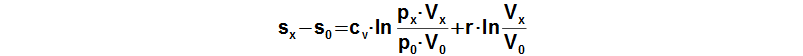
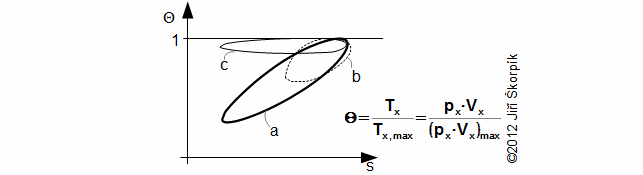
Pomocí poslední rovnice lze sestrojit T-s diagram oběhu, ze kterého lze vyhodnotit případné ztráty viz následující odstavec. U reálných motorů lze ovšem měřit velmi dobře pouze tlak, například jako funkci pootočení hřídele a objem motoru dopočítat pro konkrétní pootočení hřídele. Zjistit střední teplotu pracovního plynu v motoru a nebo hmotnost pracovního plynu v motoru, ze kterého je možné tuto teplotu dopočítat je prakticky neproveditelné. Proto se konstruuje Θ-s diagram*, kde Θ je poměr střední teploty pracovního plynu v motoru k maximu této teploty. Θ-s diagram lze sestrojit pouze z naměřeného průběhu tlaku viz níže.
Θ-s diagram z naměřených dat může ukázat na některé ztráty a nedostatky motoru:
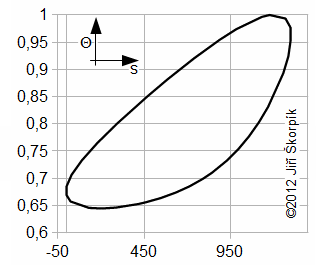 |
Úloha 3: souhrn zadání a výsledků. To, že stavu p0, V0 odpovídá minimální entropie pracovního plynu za oběh je zde čistě náhodné. |
Množství pracovního plynu lze vypočítat ze stavové rovnice ideálního plynu [2, s. 67] jako součet hmotnosti pracovního plynu v jednotlivých pracovních objemech motoru. Přičemž se vychází ze stavu, ve kterém jsou známé všechny potřebné stavové veličiny pracovního plynu. Jak je uvedeno výše měřit přesně střední teploty pracovního plynu je nesnadný úkol a pro spotřebu plynu postačí přibližný výpočet množství na základě vypočítané změny teploty pracovního plynu v motoru:
ŠKORPÍK, Jiří. Energetická bilance oběhu Stirlingova motoru, Transformační technologie, 2009-07, [last updated 2012-04]. Brno: Jiří Škorpík, [on-line] pokračující zdroj, ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/seznam-clanku.html#35. English version: Energy balance of Stirling engine cycle. Web: https://www.transformacni-technologie.cz/en_seznam-clanku.html#35.