Energetické bilance lopatkových strojů

Článek z on-line pokračujícího zdroje Transformační technologie; ISSN 1804-8293;
www.transformacni-technologie.cz; Copyright©Jiří Škorpík, 2009-2019. All rights reserved. Tato publikace neprošla redakční ani jazykovou úpravou.

● 13. Energetické bilance lopatkových strojů ●

Úvod

V lopatkových strojích může docházet ke změně entalpie, kinetické energie a potenciální energie tekutiny, podle rovnice pro První zákon termodynamiky pro otevřený systém, která platí pro všechny lopatkové stroje. V následujících kapitolách je základní popis transformace energie v různých typech lopatkových strojů, tak jak je zvykem je popisovat pro daný případ včetně vyjádření ztrát.

V kapitole Vnitřní výkon/příkon lopatkového stroje P_i je definovaná veličina měrná vnitřní práce a_i. Dalším vnitřním parametrem stroje je jeho vnitřní účinnost⁽¹⁾ η_i, která definuje efektivitu transformace energie uvnitř stroje porovnáním skutečné vnitřní práce stroje s vnitřní prací stroje beze ztrát. Rozdíl mezi měrnou vnitřní prací stroje a porovnávací měrnou ideální prací stroje jsou měrné vnitřní ztráty systému/stroje z⁽²⁾ (kinetická energie pracovní tekutiny na výstupu ze stroje se za vnitřní ztrátu stroje nepovažuje).

⁽¹⁾Poznámka
Vnitřní účinnost se u hydraulických strojů někdy označuje jako hydraulická účinnost, u tepelných strojů jako termodynamická účinnost a větrných turbín a vrtulí se vynechává slovo "vnitřní".

⁽²⁾Poznámka
Vnitřní výkon a účinnost neovlivňují pouze vnitřní ztráty, ale i netěsnost stroje viz. kapitola Ztráty nětěsností.

Energetická bilance vodní turbíny

Vodní turbíny mohou transformovat potenciální, kinetickou popřípadě tlakovou energii vody na práci a teplo – vnitřní ztráty (zvýšení vnitřní energie vody):

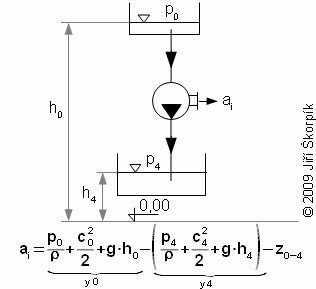1.303 Měrná vnitřní práce vodní turbíny

a_i [J·kg^-1] měrná vnitřní práce; p [Pa] tlak pracovní kapaliny; c [m·s^-1] absolutní rychlost proudění; ρ [kg·m^-3] hustota pracovní kapaliny; g [m·s^-2] gravitační zrychlení; h [m] výšky hladin; y [J·kg^-1] měrná celková energie pracovní kapaliny; z [J·kg^-1] měrné vnitřní ztráty. Odvozeno z Bernoulliho rovnice.

● 1 ●

● 13. Energetické bilance lopatkových strojů ●

Vnitřní účinnost vodní turbíny je rovna poměru mezi a_i a změně měrné celkové energie vody mezi vstupní a výstupní přírubou turbíny:

2.596 Změna měrné celkové energie vody v turbíně, hydraulická účinnost a rozdělení ztrát

Δy_1-2 [J·kg^-1] změna měrné celkové energie vody v turbíně; z_1-2 [J·kg^-1] měrné vnitřní ztráty turbíny; η_i [-] vnitřní účinnost turbíny. Rovnice pro ztráty je odvozena v Příloze 596.

Vodní turbíny patří mezi nejúčinnější lopatkové stroje s η_i až 95 %.

Vodní turbíny obvykle pohání elektrický generátor s odpovídajícím svorkovým výkonem.

Diskuze k energetickým rovnicím vodní turbíny

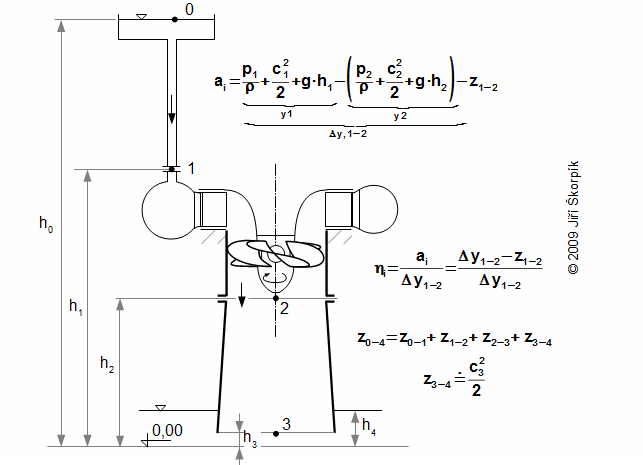
Práci pracovní kapalina koná pouze v oběžném kole a změna celkové energie vody v oběžné kole je funkcí kinetických energií a tlakového spádu na oběžné kolo (při zanedbání vlivu změny potenciální energie). Z uvedeného popisu je žádoucí, aby vodní turbína byla tvořena přetlakovým stupněm p₁>p₂ tím budou rychlosti nižší a tudíž i ztráty, které podstatně na rychlosti proudění závisí.

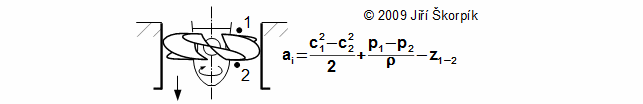
3.305 Změna měrné celkové energie v oběžném kole turbíny

● 2 ●

● 13. Energetické bilance lopatkových strojů ●

Z technických a bezpečnostních důvodů se turbíny neumísťují bezprostředně nad hladinu spodní nádrže (ohrožení turbíny zatopením atd.). Proto se u přetlakových turbín vkládá mezi turbínu a spodní nádrž sací trouba:

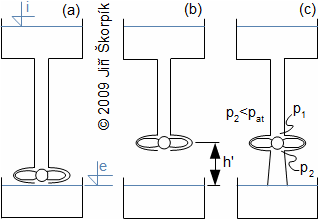
4.258 Popis funkce sací trouby

(a) turbína je těsně nad hladinou spodní nádrže – maximální využití disponibilního spádu h; (b) turbína je výše nad hladinou spodní nádrže – disponibilní spád je snížen o výšku h'; (c) sací trouba sníží tlak za turbínou, který odpovídá vodnímu sloupci h' (teoreticky zůstává zachována možnost využití disponibilního spádu h).

Sací trouba sahá těsně pod hladinu spodní nádrže a je zaplněna vodou. Její délka, respektive výška je limitována tlakovým spádem mezi koncem turbíny a tlakem nad hladinou spodní nádrže. Z principu U-trubice je zřejmé, že tlak těsně za turbínou musí být menší než tlak nad hladinou spodní nádrže. Přičemž tlak za turbínou p₂ nesmí být menší než tlak syté vody v daném bodě (tlak, při kterém voda o teplotě t₂ začne vřít). V takovém případě hrozí přetržení vodního sloupce v důsledku vzniku páry. Protože tlak p₂ je menší než tlak p₄ je měrná vnitřní práce turbíny teoreticky stejná jako pro případ turbíny bez savky umístěné těsně nad hladinou.

Vypočítejte předpokládaný vnitřní výkon a maximální délku savky vodní turbíny. Disponibilní spád 136 m, průtok 46 m³·s^-1. Neuvažujte ztráty. Řešení úlohy je uvedeno v Příloze 597.
Úloha 1.597

Energetická bilance čerpadla

Situace je obdobná jako v případě vodních turbín s tím rozdílem, že dochází k transformaci práce (vnitřní příkon čerpadla) na energii kapaliny (potenciální, kinetická, tlaková). Úkolem čerpadla je zvýšení měrné celkové energie pracovní kapaliny ze stavu y₀ na požadovaný energetický stav y₃:

● 3 ●

● 13. Energetické bilance lopatkových strojů ●

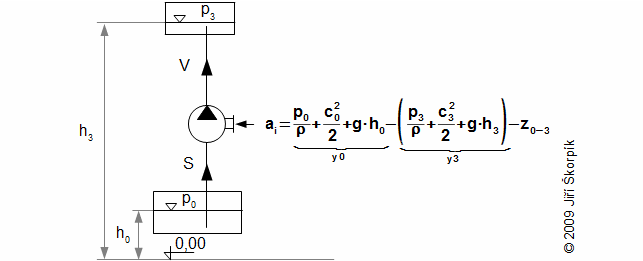
5.300 Změna celkové energie kapaliny mezi dolní a horní nádrží a vnitřní práce čerpadla

Písmeno S označuje sací stranu čerpadla (na této straně kapalina do čerpadla vstupuje), písmeno V označuje výtlačnou stranu čerpadla (na této straně kapalina z čerpadla vystupuje). Pro vnitřní práci čerpadla platí 0>a_i.

Vnitřní účinnost čerpadla je poměr změny měrné celkové energie kapaliny při průtoku čerpadlem a absolutní hodnotě měrné vnitřní práci čerpadla a_i:

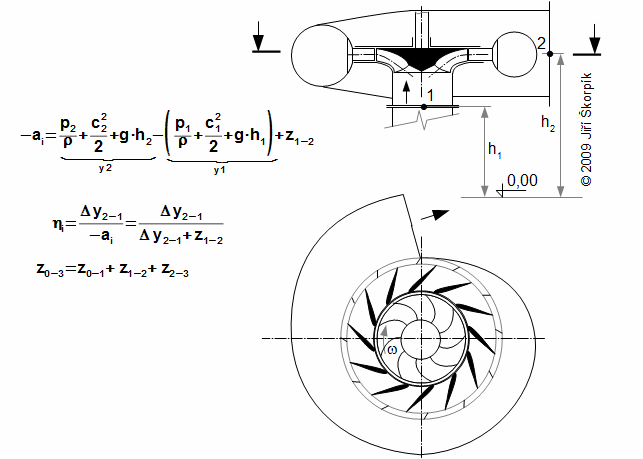
6.599 Zvýšení měrné celkové energie pracovní kapaliny v čerpadle, vnitřní účinnost a rozdělení vnitřních ztrát

Maximální η_i hydrodynamických čerpadel může být vyšší jak 90 %.

● 4 ●

● 13. Energetické bilance lopatkových strojů ●

Diskuze k energetickým rovnicím čerpadla

Při čerpání pracovní kapaliny lze často zanedbat změnu kinetické energie mezi hladinou sací a výtlačné nádrže:

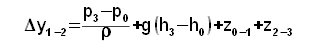7.302 Praktický výpočet zvýšení měrné celkové energie pracovní kapaliny v čerpadle

Ztráty jsou počítány z charakteristiky potrubního systému, ve kterém čerpadlo pracuje. Konec potrubní trasy je na přírubách čerpadla. Rovnice je odvozena v Příloze 302.

Energetická bilance tepelné turbíny

V tepelné turbíně probíhá transformace tepla a entalpie na práci během expanze plynu. Pracovní látka (kapalina, plyn, pára...) je ohřívána obvykle mimo turbínu, např. v případě parních turbín se pára vyrábí v parním kotli (parní oběh), v případě spalovacích turbín je horký plyn vyráběn ve spalovací komoře před turbínou (Braytonův oběh).

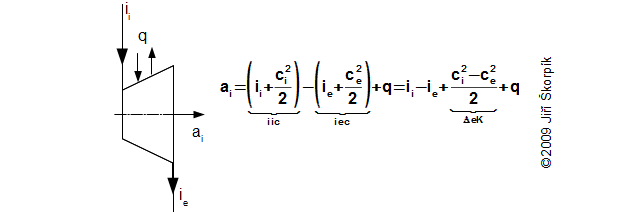
8.306 Měrná vnitřní práce tepelné turbíny

q [J·kg^-1] měrné teplo pracovního plynu sdílené s okolím; i [J·kg^-1] měrná entalpie pracovního plynu. Index i označuje vstup do turbíny; e označuje výstup z turbíny; c celkový stav. Δe_K [J·kg^-1] požadovaná změna měrné kinetické energie mezi vstupem a výstupem ze stroje (většinou je požadováno Δe_K≈0). Odvozeno z obecné rovnice pro vnitřní práci tepelného lopatkového stroje při zanedbatelné změně potenciální energie pracovního plynu.

Obvykle lze uvnitř tepelné turbíny předpokládat adiabatickou expanzi⁽³⁾ pracovního plynu, proto q=0 nebo q≈0. Ovšem existují i případy, ve kterých dochází ke sdílení tepla s okolím tzv. polytropická expanze q≠0. Případy adiabatické a polytropické expanze jsou popsány v následujících dvou kapitolách.

⁽³⁾Poznámka
V tepelných turbínách je sice vyšší teplota než je teplota okolí, ale jsou také dobře tepelně izolovány a expanze je příliš rychlá, než aby došlo ke sdílení tepla s okolím.

● 5 ●

● 13. Energetické bilance lopatkových strojů ●

Adiabatická expanze v tepelné turbíně

Plyn expanduje v turbíně z tlaku p_i na tlak p_e. Jestliže se jedná o izolovanou soustavu, musí být entropie plynu konstantní nebo se zvyšovat. Toto zvýšení entropie je způsobeno vznikem ztrátového tepla (lokálními teplotními diference vznikající například při víření a tření pracovního plynu, prouděním pracovního plynu netěsnostmi ve stupních a mísením apod.) Pro znázornění změny energetických toků v tepelných strojích se používá i-s diagram a T-s diagram:

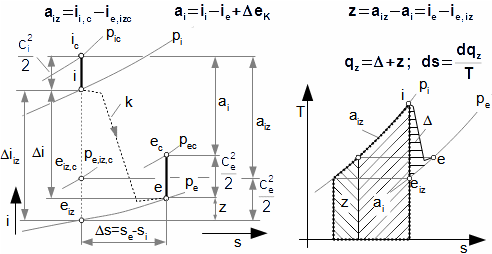
9.307 Měrná vnitřní práce tepelné turbíny při adiabatické expanzi v i-s a T-s diagramu

T [K] absolutní teplota; a_iz [J·kg^-1] měrná vnitřní práce při izoentropické expanzi (adiabatická expanze beze ztrát)⁽⁴⁾; v [m³·kg^-1] měrný objem; Δi_iz [J·kg^-1] rozdíl měrných entalpii při izoentropické expanzi; Δi [J·kg^-1] rozdíl měrných entalpii; q_z [J·kg^-1] měrné ztrátové teplo v turbíně; z [J·kg^-1] měrné vnitřní ztráty v turbíně; Δ [J·kg^-1] měrné teplo znovu využité (část q_z, které bylo v jiné části turbíny transformováno na práci); k přibližný průběh změny entalpie; s [J·kg^-1·K^-1] měrná entropie. Platí pro q=0. T-s diagram je sestrojen pro celkový stav pracovního plynu. Postup konstrukce T-s diagramu je popsán v Příloze 307.

⁽⁴⁾Poznámka
Pro porovnávácí ideální děj se obvykle očekává stejná výstupní rychlost jako při reálné expanzi c_eid=c_e. To znamená, že reálný stroj musí mít o něco větší průtočné průřezy než stroj ideální, protože ztrátové teplo měrný objem pracovního plynu zvětšuje. Takový přístup se používá i při porovnání ideální a reálné komprese.

Rozdíl měrných entalpií i_i-i_e je možné vypočítat i pomocí rovnice:

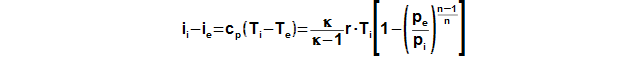
10.450 Rozdíl měrných entalpií mezi dvěma stavy

κ [-] Poissonova konstanta (konstanta izoentropy); n exponent polytropy děje (pro případ proudění beze ztrát n=κ); r [J·kg^-1·K^-1] individuální plynová konstanta; c_p [J·kg^-1·K^-1] měrná tepelná kapacita pracovního plynu při stálém tlaku. Odvozeno pro c_p=konst. Odvození rovnice je v Příloze 450.

Z předchozích rovnic je patrné, že maximální a_i adiabatické expanze jestliže se současně jedná o izoentropicku expanzi, proto se izoentropická expanze používá jako porovnávací pro stanovení vnitřní účinnosti tepelné turbíny:

● 6 ●

● 13. Energetické bilance lopatkových strojů ●

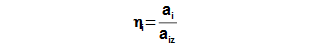11.604 Vnitřní účinnost tepelné turbíny vztažená k izoentropickému ději.

Maximální η_i některých tepelných turbín přesahuje 90 % (u parních turbín 92 % – v případě vícetělesových parních turbín může být vnitřní účinnost jednotlivých tělesech rozdílná).

Vypočítejte vnitřní výkon parní turbíny a skutečnou suchost páry na konci expanze. Průtok páry turbínou je 33 t·h^-1, vnitřní účinnost turbíny je 75 %, měrná izoentropická práce turbíny je 1 259,59 kJ·kg^-1, tlak na výstupu z turbíny je 3 kPa, tlak a teplota na vstupu do turbíny jsou 3,5 MPa, 450 °C. Řešení úlohy je uvedeno v Příloze 871.
Úloha 2.871

Polytropická expanze v tepelné turbíně

V některých případech expanzi v turbínách ovlivňuje sdílení tepla s okolím, například chlazení teplotně exponovaných částí turbíny apod. V takových případech je expanze podobná polytropické expanzi.

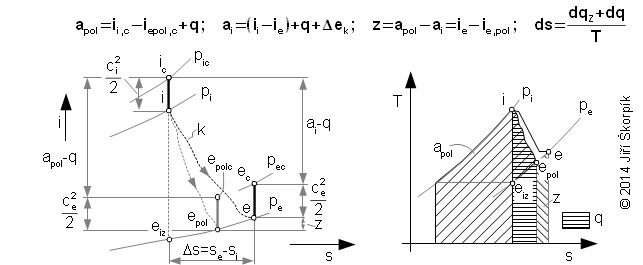
12.685 Měrná vnitřní práce turbíny pro případ q>0

e_pol stav plynu na výstupu ze stroje při vratné polytropické expanzi. a_pol [J·kg^-1] měrná vnitřní práce při vratné polytropické expanzi⁽⁵⁾ (expanze beze ztrát) při stejném teplu q. T-s diagram je sestrojen při zanedbání rozdílu měrných kinetických energií. Postup konstrukce T-s diagramu je popsán v Příloze 685.

⁽⁵⁾Vyjádření plochy v T-s diagramu ekvivalentní práci plynu při expanzi.: Plocha představující teplo q se od plochy a_pol odečítá, jestliže je q<0 a naopak. Plocha představující změnu entalpie při izobarické změně (i_e-i_e,pol) se od plochy a_pol odečítá, jestliže i_e-i_e,pol>0 a naopak.

● 7 ●

● 13. Energetické bilance lopatkových strojů ●

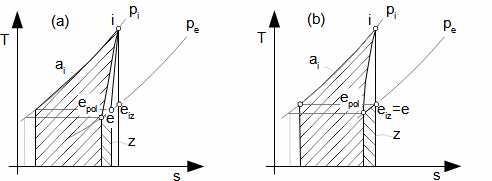
13.686 Vnitřní práce turbíny s chlazenou expanzí q<0

(a) případ kdy e_iz>e; (b) případ kdy e_iz=e (zdánlivě izoentropická expanze). T-s diagram je sestrojen při zanedbání rozdílu měrných kinetických energií.

Pro případ polytropické expanze je maximální a_i dosaženo při vratné polytropické expanzi, proto se vratná polytropická expanze používá jako porovnávací pro stanovení vnitřní účinnosti tepelné turbíny při polytropické expanzi:

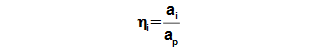14.908 Vnitřní účinnost tepelné turbíny vztažená k vratné polytropické expanzi

a_p [J·kg^-1] měrná práce při porovnávací (navržené) ideální polytropické expanzi (obvykle izotermická expanze).

Výše uvedené poznatky lze aplikovat i na popis expanze se sdílením tepla s okolím v jednom stupni tepelné turbíny.

Energetická bilance turbokompresoru

V kompresoru probíhá transformace práce na tlakovou energii pracovního plynu.

15.117 Měrná vnitřní práce turbokompresoru

Je zřejmé, že a_i<0. Odvozeno z obecné rovnice pro vnitřní práci tepelného lopatkového stroje při zanedbatelné změně potenciální energie pracovního plynu.

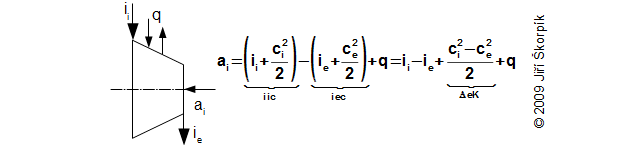
Obvykle lze uvnitř kompresoru předpokládat adiabatickou kompresi pracovního plynu, proto q=0 nebo q≈0. Ovšem existují i případy, ve kterých dochází ke sdílení tepla s okolím tzv. polytropická komprese q≠0. Případy adiabatické a polytropické komprese jsou popsány v následujících dvou kapitolách.

● 8 ●

● 13. Energetické bilance lopatkových strojů ●

Adiabatická komprese v kompresoru

Plyn je komprimován v turbokompresoru mezi tlakem na vstupu do turbokompresoru p_i a tlakem na výstupu z turbokompresoru p_e. Podobně jako u expanze plynu v tepelné turbíně (viz popis nad Rovnicí 9), tak i v turbokompresoru vzniká měrné ztrátové teplo q_z, které způsobuje zvyšování entropie pracovního plynu:

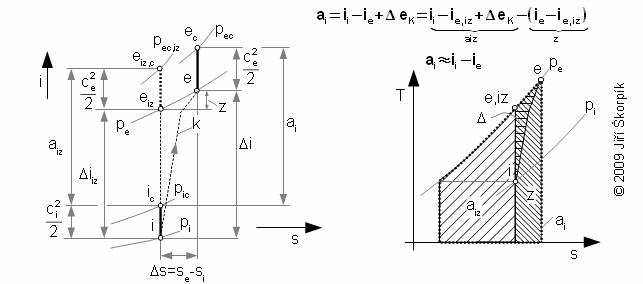
16.118 Měrná vnitřní práce turbokompresoru při adibatické kompresi v i-s a T-s diagramu

z [J·kg^-1] měrné vnitřní ztráty (práce, kterou je třeba přivést navíc oproti vratné adiabatické kompresi beze ztrát); Δ [J·kg^-1] měrné přídavné ztráty; k přibližný průběh komprese. Platí pro q=0. T-s diagram je sestrojen pro celkový stav pracovního plynu. Rovnice jsou odvozeny v Příloze 118.

Jestliže není znám i-s diagram pracovního plynu lze použít pro rozdíl entalpií i_i-i_e Rovnici 10.

Pro adiabatickou kompresi je maximální a_i dosaženo při izoentropické kompresi, proto se izoentropická komprese používá jako porovnávací při stanovení vnitřní účinnosti kompresoru při adiabatické kompresi:

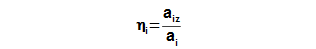17.609 Vnitřní účinnost kompresoru při adiabatické kompresi

Průměrná η_i se pohybuje kolem 80 %, ale nejlepší konstrukce dosahují 89 až 91 %.

Důležitým parametrem je i kompresní poměr turbokompresoru vycházejích ze statických nebo celkových tlaků:

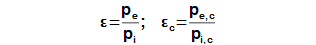18.610 Kompresní poměr kompresoru

ε [-] kompresní poměr.

Turbokompresor je poháněn nejčastěji el. motorem, spalovací turbínou nebo turboexpandérem. V průmyslových provozech, ve kterých je vysoká spotřeba stlačeného plynu bývá poháněn parní turbínou.

● 9 ●

● 13. Energetické bilance lopatkových strojů ●

Polytropická komprese v kompresoru

V některých případech kompresi v kompresorech ovlivňuje sdílení tepla s okolím. Například při chlazení kompresoru. V takových případech je komprese podobná polytropické kompresi.

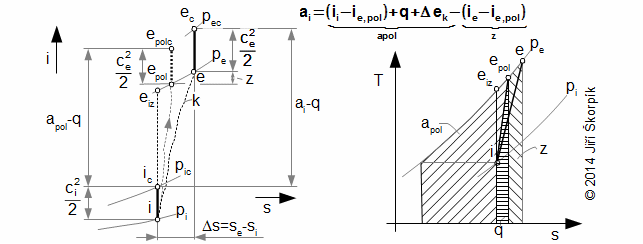
19.687 Měrná vnitřní práce kompresoru pro případ q>0.⁽⁶⁾

e_q stav pracovního plynu na výstupu ze stroje, kdy v průběhu komprese bylo přiváděno teplo q a komprese probíhala beze ztrát. T-s diagram je sestrojen při zanedbání rozdílu měrných kinetických energií. Odvození je uvedeno v Příloze 687.

⁽⁶⁾Vyjádření plochy v T-s diagramu ekvivalentní práci plynu při kompresi: Ideální polytropická práce kompresoru a_pol má záporné znaménko, proto při hledání ekvivalentní práce kompresoru a_i platí pro jednotlivé plochy: plocha představující teplo q se od plochy a_pol odečítá, jestliže je q>0 a naopak. Plocha představující změnu entalpie při izobarické změně (i_e-i_e,pol) se od plochy a_pol odečítá, jestliže je i_e-i_e,pol<0 a naopak.

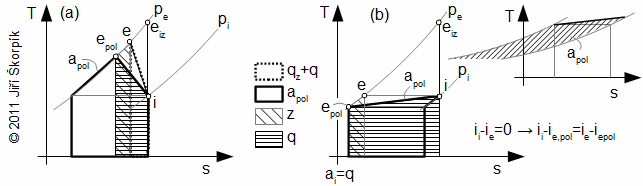
20.688 Měrná vnitřní práce kompresoru pro případ q<0

(a) případ kdy z<-q; (b) případ kdy T_e=T_i (zdánlivě izotermická komprese⁽⁷⁾). T-s diagram je sestrojen při zanedbání rozdílu měrných kinetických energií.

⁽⁷⁾Poznámka
Teplota chladícího média musí být v tomto případě nižší než teplota pracovního plynu na vstupu do kompresoru T_i.

● 10 ●

● 13. Energetické bilance lopatkových strojů ●

Pro polytropickou kompresi je maximální a_i dosaženo při vratné polytropické kompresi, proto se vratná polytropická komprese používá jako porovnávací při stanovení vnitřní účinnosti kompresoru při polytropické kompresi:

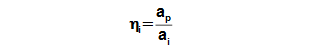21.1003 Vnitřní účinnost kompresoru vztažená k vratné polytropické kompresi

a_p [J·kg^-1] měrná práce při porovnávací (navržené) ideální polytropické kompresi (a_p≠a_pol, protože velikost a_pol ovlivňují ztráty při reálné kompresi viz úloha [26.612]).

Výše uvedené poznatky lze aplikovat i na popis komprese se sdílením tepla s okolím v jednom stupni lopatkového stroje.

Energetická bilance ventilátoru

Ventilátory jsou stroje, které zajišťují nucené proudění plynů (překonání tlakových ztrát) s malým zvýšením tlaku. Při výpočtu ventilátorů se často zavádí předpoklad nestlačitelného proudění ρ≈konst., t≈konst. Práce dodávaná proudícímu plynu se transformuje na tlakovou a kinetickou energii, změna potenciální energie ve ventilátoru je zanedbatelná. Protože kompresní poměr ε_c ventilátoru je velmi malý je lepší transformaci energie popisovat na základě zvýšením celkového tlaku plynu Δp_c, takže z Bernoulliho rovnice lze odvodit:

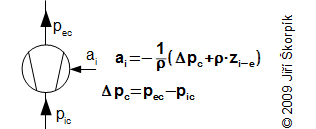22.309 Měrná vnitřní práce ventilátoru

Δp_c [Pa] zvýšení celkového tlaku ve ventilátoru. Předpoklad: zanedbání změny potenciální energie. Rovnice je odvozena v Příloze 309.

Vnitřní účinnost ventilátoru se definuje jako poměr měrné vnitřní práce ventilátoru beze ztrát a měrné vnitřní práci ventilátoru:

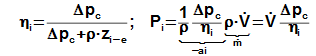23.581 Vnitřní účinnost a příkon ventilátoru

V^• [m³·s^-1] objemový průtok; m˙ [kg·s^-1] hmotnostní průtok ventilátorem.

● 11 ●

● 13. Energetické bilance lopatkových strojů ●

Energetická bilance větrné turbíny

Ve větrné turbíně se transformuje část kinetické energie větru, který proudí přes turbínu, na práci (je zanedbáván vliv změn potenciální, vnitřní tepelné a tlakové energie). Vlivem snížení kinetické energie větru je za turbínou proud pomalejší a z rovnice kontinuity dojde ke zvětšení průřezu proudové trubice. Proud vzduchu za turbínou se stává překážkou pro okolní proudění (proudění mimo proudovou trubici), které ji pozvolně obtéká. Z těchto příčin vzniká proudová trubice (oddělení proudu vzduchu proudící přes rotor od ostatního proudění) daleko před turbínou. Měrnou práci větrné turbíny je měrná práce vzduchu uvnitř proudové trubice rotoru:

24.311 Transformace energie v rotoru větrné turbíny-axiální stupeň

P.T. proudová trubice rotoru. Odvozeno z Bernoulliho rovnice.

Axiální stupeň větrné turbíny je přetlakový. Rozšiřující se proud vzduchu před turbínou funguje jako difuzor, kde se kinetická energie přeměňuje na tlakovou energii. Rozšiřující se proud vzduchu za turbínou funguje podobně jako sací trouba u vodní turbíny (těsně za turbínou vzniká podtlak):

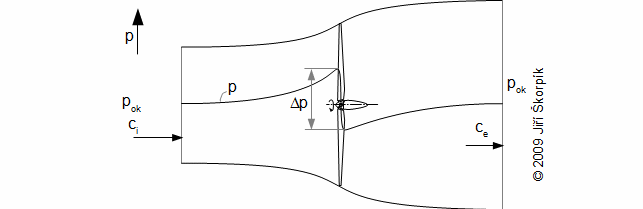
25.615 Průběh tlaku v proudové trubici rotoru axiálního stupně větrné turbíny

p_ok [Pa] tlak vzduchu na vstupu a výstupu proudové trubice; Δp [Pa] rozdíl tlaku na rotoru.

Účinnost větrné turbíny η_i se vypočítá jako poměr měrné práce a_i ku měrné optimální práci větrné turbíny. Měrné optimální práce větrné turbíny je dosaženo při snížení absolutní rychlosti větru o dvě třetiny po průchodu proudovou trubicí:

● 12 ●

● 13. Energetické bilance lopatkových strojů ●

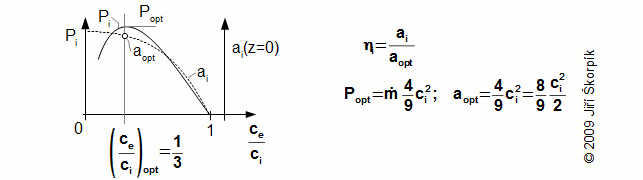
26.313 Měrná optimální práce větrné turbíny a její účinnost

P_opt [W] optimální výkon větrné turbíny; a_opt [J·kg^-1] měrná optimální práce větrné turbíny; m^• [kg·s^-1] množství vzduchu protékající rotorem. Rovnice jsou odvozeny v Příloze 313.

Vrtule

Vrtule, lodní šrouby a pod. jsou lopatkové stroje bez skříně a transformace energie probíhá podobně jako u větrných turbín. Proud pracovní tekutiny získává při průchodu rotorem kinetickou energii, což zvyšuje její rychlost:

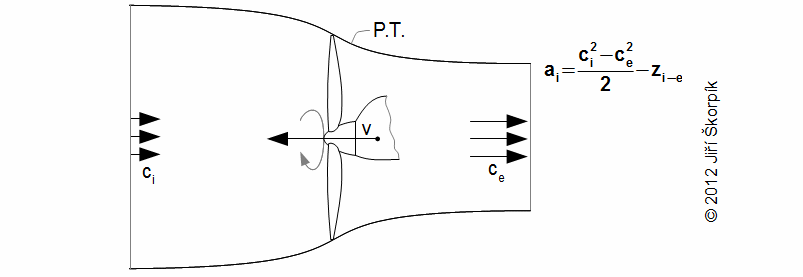
27.886 Transformace energie v rotoru vrtule

v [m·s^-1] rychlost axiálního pohybu vrtule vzhledem k vztažné soustavě, ke které jsou vztaženy i absolutní rychlosti c_i a c_e. Odvozeno z Bernoulliho rovnice.

Vrtule slouží k vytvoření tahu – síla, která se využívá k uvedení letounu do pohybu, nebo při rovnoměrném pohybu k překonání aerodynamického odporu a tíhových sil. Hlavní funkcí vrtule je tedy vytvářet tah:

● 13 ●

● 13. Energetické bilance lopatkových strojů ●

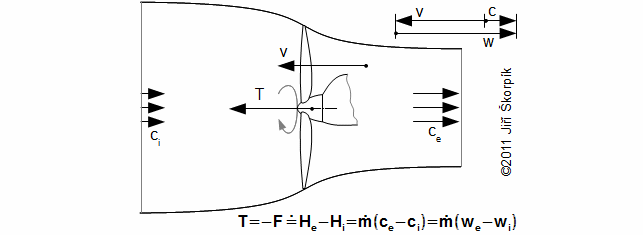
28.177 Tah vrtulového pohonu

T [N] tah vrtulového pohonu (kladný směr ve směru pohybu); F [N] síla, kterou působí proudící látka na kontrolní objem (proudová trubice vrtule); w [m·s^-1] relativní rychlost proudící látky. Rovnici pro tah lze odvodit pomocí Eulerovy rovnice. Tlakové síly na vstupu i výstupu z proudové trubice vrtule se vzájemně vyruší a vliv hmotnostních sil je zanedbatelný. Rovnice je odvozena pro případ, kdy směr letu je rovnoběžný se směrem proudění (v // c). Odvození je také provedeno např. v [1].

Rozhodující veličinou vrtulového pohonu je tah T, který umožňuje letounu let rychlostí v, proto je účinnost vrtule vztažena k těmto dvěma veličinám. Účinnost vrtule vyjadřuje efektivitu transformace práce (příkonu) na tah, účinnost využití změny kinetické energie relativních rychlostí proudu vzduchu na vytvoření tahu se nazývá propulzní účinnost:

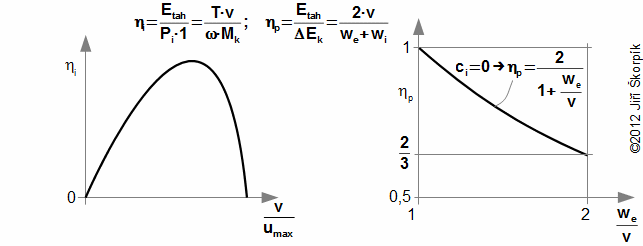
Účinnost vrtule a propulzní účinnost vrtulového pohonu

29.890 Účinnost vrtule a propulzní účinnost vrtule

E_tah [J·s^-1] práce vykonaná tahem za jednu sekundu letu; P_i·1 [J] práce pohonu za jednu sekundu letu; ω [rad·s^-1] úhlová rychlost otáčení vrtule; M_k [N·m] kroutící moment přenášený na vrtuli; η_p [-] propulzní účinnost vrtule; ΔE_K [J·s^-1] změna kinetické energie vzduchu v proudové trubici vrtule za jednu sekundu letu. Rovnice jsou odvozeny v Příloze 890.

Při optimálních podmínkách letu dosahuje účinnost vrtule η_i více jak 90 % a účinnost η_p cca 85 % [2, s. 613].

reklama

Návrhové programy lopatkových strojů – VIKLAN – výpočtové programy na míru

● 14 ●

● 13. Energetické bilance lopatkových strojů ●

Odkazy

1. Unified Propulsion, 2011. [Online] kurz v rámci projektu MIT OpenCourseWare Massachusetts Institute of Technology. Adresa: http://ocw.mit.edu.

2. MATTINGLY, Jack, HEISER, William, PRATT, David. Aircraft Engine Design, 2002. Second edition. Reston: American Institute of Aeronautics and Astronautics, ISBN 1-56347-538-3.

3. KADRNOŽKA, Jaroslav. Teorie lopatkových strojů, 1991. 3. vydání, přepracované. Brno: Vysoké učení technické v Brně, ISBN 80-214-0275-X.

4. KRBEK, Jaroslav. Tepelné turbíny a turbokompresory, 1990. 3. vydání. Brno: Vysoké učení technické v Brně, ISBN 80-214-0236-9.

Bibliografická citace článku

ŠKORPÍK, Jiří. Energetické bilance lopatkových strojů, Transformační technologie, 2009-10, [last updated 2018-11-16]. Brno: Jiří Škorpík, [on-line] pokračující zdroj, ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/13.html. English version: Energy balances of turbomachines. Web: https://www.transformacni-technologie.cz\en_13.html.

● 15 ●