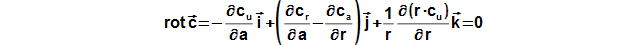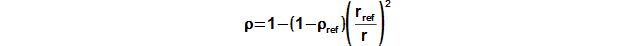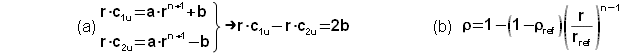NÁVRH AXIÁLNÍCH STUPŇŮ LOPATKOVÝCH STROJŮ

Úvod

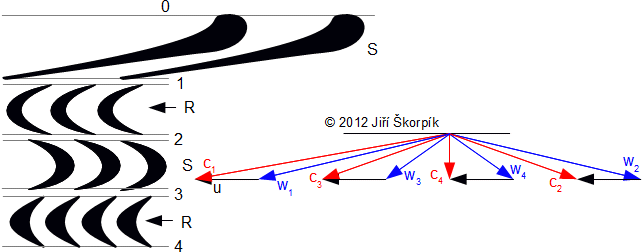
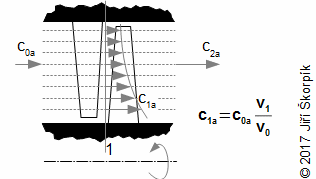
Výsledkem návrhu axiálního lopatkového stroje mohou být tvarově jednoduché stupně s přímými lopatkami, které nezohledňují prostorový charakter proudění nebo naopak stupně se zkroucenými lopatkami⁽¹⁾, které tento charakter proudění více či méně zohledňují. Postup návrhu ovlivňují požadované náklady na výrobu a vnitřní účinnost stupně. Tyto požadavky mohou vést na dosti odlišný výsledek.

⁽¹⁾Zkroucená lopatka

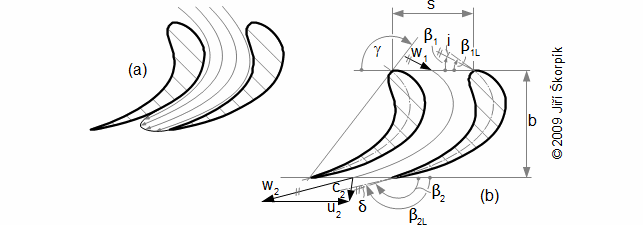
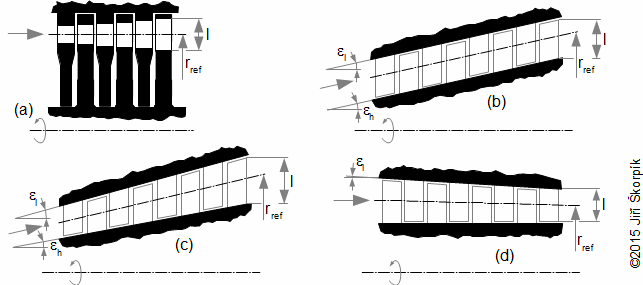
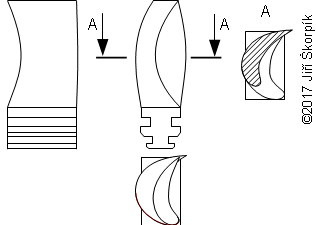
Jedná se o typ lopatky se změnou úhlu nastavení profilu v mříži po výšce lopatky a většinou i tvarem profilu. Při návrhu zkroucené lopatky se přihlíží k prostorovému charakteru proudění ve stupni (tj. ke změně obvodové rychlosti, stupně reakce a stavových veličin pracovní tekutiny po výšce lopatky). Výsledný tvar lopatek je složitý a přináší zvýšené výrobní náklady (obvykle se vyrábí na 5-osé frézce z tvarového odlitku, ale jsou i jiné technologie výroby pro duté lopatky) oproti tvarově přímým (prizmatickým) lopatkám. Silně zkroucené a dlouhé rotorové lopatky působením odstředivých sil podléhají rozkrucování. To se v současné době řeší integrovaným tlumičem vibrací lopatek, který se zaklesne do tlumiče vibrací sousední lopatky až při určitých otáčkách stroje a tím dojde ke zpevnění lopatkové mříže a zastavení dalšího rozkrucování lopatek. Je tedy nutné počítat s tím, že geometrie profilu bude při klidu stroje jiná než při jmenovitých otáčkách:

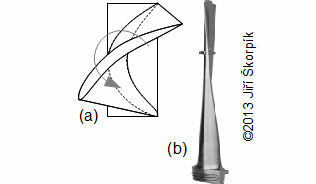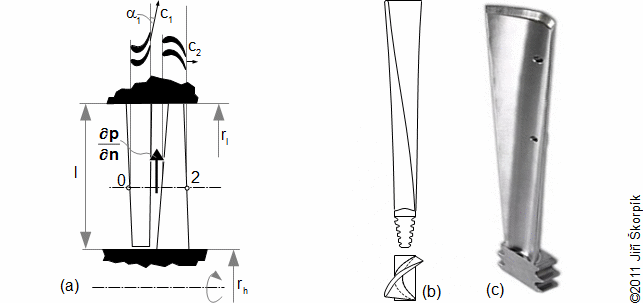
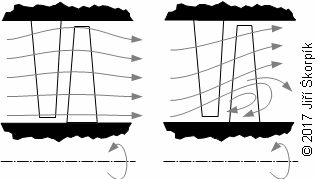
1.948 Rozkrucování dlouhé a silně zkroucené lopatky (a) znázornění směru rozkrucování silně zkroucené lopatky působením odstředivých sil; (b) silně zkroucená lopatka s integrovaným tlumičem vibrací (obrázek z [8]).

Tento článek se zaměřuje na stupně lopatkových strojů se skříní a nikoliv na návrh stupňů strojů bez skříně jako jsou větrné turbíny, vrtule a lodní šrouby. Popis návrhu větrné turbíny je proveden v kapitole Aerodynamický návrh větrné turbíny.

Cíle a zjednodušující předpoklady návrhu

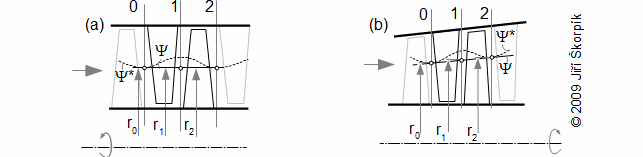
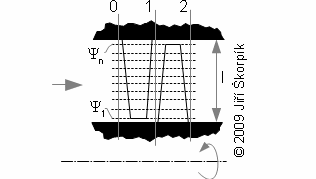
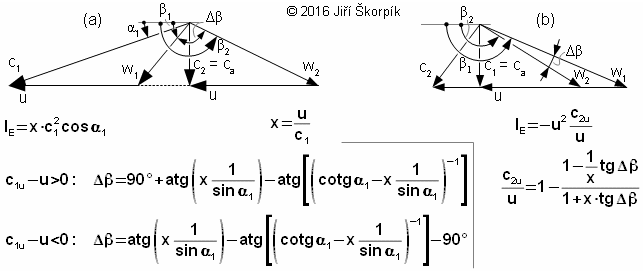
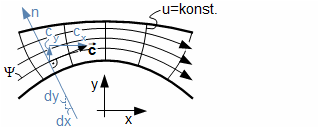
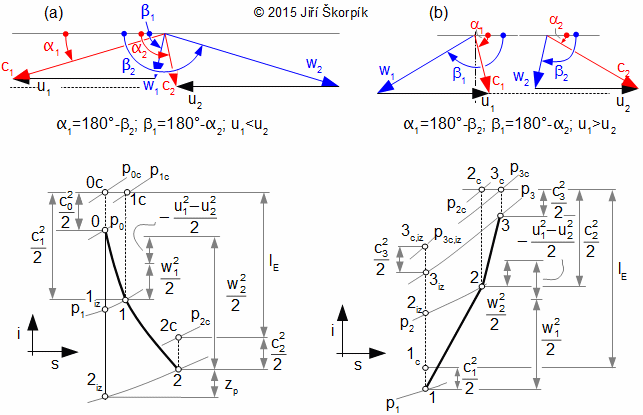
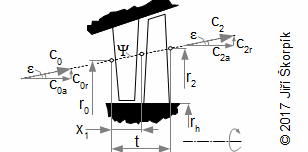
Obecným cílem návrhu stupně lopatkového stroje je především určení geometrických a aerodynamických veličin lopatkové mříže, která přímo vychází z očekávané trajektorie proudnic, respektive rychlostního trojúhelníku, pro které se následně hledá nejvhodnější profil lopatky. Protože trajektorie proudnic je v prostoru stupně složitá, zavádí se zjednodušující předpoklad proudění po válcových nebo kuželových plochách⁽²⁾. Toto zjednodušení umožňuje stupeň řešit analyticky:

2.348 Zjednodušená trajektorie proudění v axiálním stupni

Zkroucené lopatky se musí navrhovat na několika poloměrech, přičemž na každém z nich je nutné provést návrh rychlostního trojúhelníku⁽³⁾, stupně reakce a energetickou bilanci:

3.329 Způsob rozdělení stupně do několika řezů za účelem vypočtu l [m] délka lopatek. Na obrázcích je rozdělení do n elementů. Takže výsledek výpočtu na každém poloměru je ideálně platný pouze v okolí tohoto poloměru o elementární tloušťce dr, proto se geometrie stupně na takovém poloměru nazývá elementární stupeň lopatkového stroje.

Rychlosti pro rychlostní trojúhelník se počítají z otáček, poloměru lopatek a z obvodové práce, která vychází z celkové energetické bilance stupně. Rychlostní trojúhelník proudnice v blízkosti profilu lopatky je jiný (v důsledku profilových ztrát) než ve středu lopatkového kanálu, proto se vychází z rychlostního trojúhelníku, jenž odpovídá střední rychlosti tekutiny v lopatkovém kanálu elementárního stupně⁽⁴⁾. Takže proudnice v lopatkovém kanálu se nahradí jedinou.

4.316 Geometrické a aerodynamické charakteristiky lopatkového kanálu na vyšetřovaném poloměru

Jsou-li na jednotlivých poloměrech vypočítané optimální úhly rychlostí i lopatek přistupuje se k výběru vhodného profilu lopatky. V tomto bodě zná výpočtář geometrii stupně a na základě aerodynamiky takové geometrie (viz. článek Základy aerodynamiky profilů lopatek a lopatkových mříží) lze vypočítat skutečné ztráty ve stupni (viz. článek Ztráty v lopatkových strojích), které musely být v prvním kroku odhadnuty pomocí podobnostních součinitelů⁽⁶⁾. Pokud odhady ztrát nesedí s výpočtem musí být proveden nový návrh stupně.

Uvedený postup neříká nic o výběru typu stupně či spádu apod. To by mělo být součást zadání pro návrh stupně.

Po dokončení výpočtu geometrie stupně se provádí pevnostní výpočet lopatek, přirozeně se zpětnou vazbou na výpočet geometrie. Při výpočtu se vychází ze skutečných sil působících na lopatky od proudu tekutiny jejichž výpočet je popsán v kapitole Stanovování aerodynamických veličin lopatkových mříží. Pevnost lopatky má samozřejmě přednost před ideálním aerodynamickým návrhem lopatky – to se projevuje především u dlouhých zkroucených lopatek.

Přehledné je provést výpočet stupně nejdříve pro ideální proudění ideální tekutiny. Takto konstruktér hned na začátku získá představu o velikosti a parametrech stupně a minimálnímu nutnému počtu odhadů a typů kritérií podobnosti. Také může přesněji odhadnout, pro finální iterační výpočet, velikost ztrát z geometrie stupně a rychlostí, protože především na rychlostech záleží většina ztrát. Také může lépe posoudit vliv těchto ztrát na geometrii stupně.

Zde popsané cíle a metody návrhu stupně nejsou univerzální, protože existuje velmi mnoho variant zadání, například se může jednat o vylepšení stupně renovovaného stroje, kontrolní výpočet apod., jedná se ale o postup obvyklý při návrhu zcela nového stroje.

Optimální rychlostní trojúhelníky axiálních stupňů

Optimální je ten, který splňuje zadání. Obecným cílem je navrhnout takový rychlostní trojúhelník stupně, který bude mít požadovanou obvodovou práci při co nejmenších ztrátách, respektive se snaží o co největší obvodovou účinnost stupně. Samozřejmě mohou existovat i přednostnější požadavky vyplývající z funkce stupně či pevnostních limitů. Požadavky na rychlostní trojúhelníky jednostupňových strojů mohou být jiné než požadavky na stupně vícestupňových strojů.

Rychlostní trojúhelníky se nejčastěji více či méně blíží dvěma základním optimům. U turbínových stupňů je snahou dosáhnout co nejnižší výstupní rychlosti c₂ (nejmenší ztráta výstupní rychlosti) a současně vysokou hodnotu obvodové složky vstupní rychlosti c_1u, respektive co nejmenší úhel vstupní rychlosti α₁ (nejčastěji se tento úhel pohybuje v rozmezí 8° až 16°). U stupňů pracovních strojů je požadavkem i vysoké zvýšení tlaku ještě v rotorových lopatkových kanálech, protože difuzorové lopatkové kanály jsou citlivější na různé profilové ztráty, je požadováno současně i malé zakřivení proudu Δβ (nejčastěji se tento úhel pohybuje v rozmezí 15° až 30°). Pro takto definované stupně lze odvodit jednoduché rovnice pro zakřivení proudu jako funkce jednotlivých rychlostí:

5.801 Rovnice optimálních rychlostních trojúhelníků axiálních stupňů

Výše uvedené rovnice mohou sloužit jako orientační vodítka při návrhu stupňů a výběr profilů lopatek. Tyto rovnice jsou také zpracovány v Nomogramech 320, 431.

Stupně s přímými lopatkami

Z pohledu geometrie stupně se jedná o nejjednodušší typ stupně, protože jeho geometrie se nemění. Z toho důvodu nemá smysl počítat stupeň na několika poloměrech, ale pouze na jednom tzv. referenčním poloměru, na kterém jsou parametry proudění co nejblíže průměrným hodnotám v rámci celého stupně. Referenčním poloměr bývá nejčastěji střední poloměr lopatek nebo střední kvadratický poloměr⁽⁷⁾:

6.267 Referenční poloměry axiálního stupně (a) rovnice pro střední poloměr lopatek; (b) rovnice pro kvadratický poloměr lopatek; (c) rovnice pro výpočet referenční délky lopatky axiálního stupně; (c) rovnice pro výpočet referenční délky lopatky. Index ref označuje referenční, l poloměr lopatek na špici, h poloměr hřídele. Odvození referenčních poloměrů axiálního a diagonálního stupně je uvedeno v Příloze 267.

⁽⁷⁾Střední kvadratický poloměr

Střední kvadratický poloměr je takový poloměr, na kterém platí, že plocha mezikružím mezi r_l a r_ref je stejně velká jako plocha mezikruží mezi r_ref a r_h.

Výhodou stupně s přímými lopatkami není jen méně rozsáhlý výpočet ale především menší výrobní náklady, včetně použití méně jakostních ocelí než u lopatek kroucených, protože snesou vyšší zatížení bez deformace. Nevýhodou stupňů s přímými lopatkami je nižší vnitřní účinnost stupně oproti lopatkám zkrouceným, které zohledňují prostorový charakter proudění ve stupni viz popis v dalších kapitolách. Pokles vnitřní účinnosti stupně se projevuje s rostoucím poměrem l·r^-1.

Použití axiálního stupně s přímými lopatkami je oprávněné u stupňů, kde projev prostorového charakteru proudění není velký, například u axiálních stupňů se jedná o stupně l·r^-1<0,14..0,2 [7, s. 153]. Ovšem uvedený rozsah (především vyšší čísla) v současně době není tolik aktuální. Vzhledem ke zrychlení výpočtu stupně, které umožňuje použití výpočetní techniky se i velmi krátké lopatky počítají s ohledem na prostorový charakter proudění. Větší vliv má ale obrovské snížení rozdílu v nákladech na výrobu lopatky zkroucené oproti přímé lopatce, které dříve byly i o dva řády rozdílné (vytvoření dokumentace, modelu, ruční dokončovací práce a pod.).

Přímé lopatky se obecně používají na strojích, kde více záleží na pořizovacích nákladech než na účinnosti (stroje provozované jen zřídka, obvykle na krátkou dobu, záložní stroje, stroje s vysokým opotřebením a nutností časté výměny lopatek), stroje s malým objemovým průtokem a jako počáteční stupně turbín či poslední stupně kompresorů, kde jsou lopatky velmi krátké a převažuje jiný typ ztrát než ty spojené s ignorováním prostorového charakteru proudění.

Axiální stupně s přímými lopatkami lze navrhnout ve třech základních variantách a to jako rovnotlaký stupeň, Curtisův stupeň a přetlakový stupeň:

Návrh axiálního rovnotlakého stupně turbíny

Rovnotlaký stupeň s přímými lopatkami se používá u tepelných turbín, ale není vhodný pro kompresory kvůli vysokým rychlostem na vstupu do statoru a velkému prohnutí střední čáry profilu lopatky, která zvyšuje citlivost na ztrátu vířením při odtržení mezní vrstvy od profilu. Rovnotlaké stupně se také používají u axiálních ventilátorů, kde se zakřivení snižuje zkrácením délky odtokové hrany lopatky viz kapitola Axiální ventilátory.

Hlavním charakteristickým znakem rovnotlakého stupně je přibližně stejný tlak před i za rotorovou řadou lopatek a tedy i nule blízký stupeň reakce. To má konstrukční i termodynamické výhody. Mezi konstrukční patří malá síla působí na rotorovou řadu lopatek, která je rovna pouze odporové síle od proudu tekutiny. To vede na nízké ztráty i v axiálním ložisku rotoru a to i v případě diskové koncepce rotoru, která se používá u jednostupňových strojů např. jednostupňová parní Lavalova turbína nebo jednostupňový axiální ventilátor, kde tlak na obou stranách disku rotoru je stejný, takže u jednostupňového přetlakového stupně by byly axiální síly výrazně vyšší. Termodynamickou výhodou je relativně vysoký zpracovaný entalpický spád ve stupni oproti přetlakovému stupni viz porovnání axiálních stupňů na konci kapitoly.

Nevýhodou je vysoká rychlost proudění na výstupu ze statorové řady lopatek v případě turbínových stupňů nebo naopak na vstupu do statorové řady lopatek v případě stupňů pracovních strojů. To významně zvyšuje profilové ztráty, které rostou s druhou mocninou rychlosti. U turbínových stupňů se proto pro snížení těchto ztrát rovnotlaké stupně často konstruují s mírným stupněm reakce o velikosti 0,03 až 0,06 [10, s. 91] tedy s mírným přetlakem p₁>p₂. Stupeň reakce by měl být takový aby přinesl snížení profilových ztrát, ale současně zůstaly zachovány výhody axiálního stupně.

U vícestupňových turbín je navíc požadavek na splnění podmínek normálního stupně c₀=c₂ při v₀<v₂ (v-měrný objem). Takový požadavek vede na to, že lopatky rotoru jsou delší než statoru (viz. Obrázek 18). Rychlost c₁ je velmi vysoká a proto požadujeme-li co nejnižžší ztrátu výstupní rychlosti musíme počítat s nerovností c_2a<c_1a. U tepelených jednostupňových rovnotlakých turbín, bývá ztráta výstupní rychlostí velmi vysoká, protože malé výstupní rychlosti by vedly na velké rozdíly délek statorových a rotorových lopatek. Současně při vzniku profilových ztrát u rovnotlakého stupně musíme očekávat, že relativní rychlost na výstupu z lopatkové mříže musí být menší než vstupní⁽⁸⁾ w₂<w₁, takže typický trojúhelník rovnotlakého stupně vypadá asi takto:

7.70 Válcový řez rovnotlakého axiálního stupně s malým stupněm reakce a jeho rychlostní trojúhelník

S malým stupně reakce by i-s diagram axiálního stupně tepelné turbíny vypadal následovně:

8.351 i-s diagram rovnotlakého stupně tepelné turbíny

Optimální návrh stupně se provádí podle kritérií podobnosti, především se používá průtokový součinitel a rychlostní poměr, který je důležitý pro prvotní odhad optimálních parametrů stupně:

9.352 Přibližné optimální parametry rovnotlakého axiálního stupně tepelné turbíny

Jestliže je tlakový poměr na statoru menší než kritický tlakový poměr musí lopatky statoru vytvářet lopatkový kanál tvarově podobný Lavalově trysce, který je vhodný pro nadzvukové rychlosti proudění. Takové řešení se nejčastěji vyskytuje u  jednostupňových parních turbín a turboexpandérů plynu.

Návrh Curtisova stupně

Curtisův stupeň je speciálním případem rovnotlakého stupně, používá se jako vhodnější varianta jednostupňových tepelných turbín s vysokým entalpickýcm spádem, který vede na velmi vysoké rychlosti (často až na nadzvukové) a tedy i profilové ztráty. V tomto případě se disponibilní energie také transformuje na kinetickou energii ve statorové řadě lopatek, ale potom proudí více jak jednou řadou lopatek rotorových mezi kterými je vložena další rovnotlaká statorová lopatková řada, která pouze mění směr proudění. Podle toho kolik takový stupeň obsahuje rotorových řad se nazývá Curtisův dvouvěncový, třívěncový stupeň atd. Curtisův jednověncový stupeň je klasický axiální rovnotlaký stupeň:

10.913 Válcový řez Curtisovým stupněm a jeho rychlostní trojúhelník

Výhoda Curtisova stupně je, že dokáže zpracovat, při optimální účinnosti, vyšší rozdíl entalpií než jeden stupeň rovnotlaký, který by navíc musel mít při stejném průměru daleko vyšší otáčky jak plyne s následujících rovnic:

11.950 Přibližné optimální parametry Curtisova dvouvěncového stupně

Curtisův dvouvěncový stupeň dokáže zpracovat přibližně 4x větší rozdíl entalpie ve stupni při optimálních podmínkách než axiální stupeň rovnotlaký, ale za cenu horší obvodové účinnosti, protože rychlosti, a tedy i profilové ztráty, jsou velmi vysoké (expanze probíhá jen v první statorové řadě) viz porovnání Rovnice 9. a Rovnice 11. Pro zvýšení obvodové účinnosti Curtisova stupně se konstruují jednotlivé lopatkové řady s mírným přetlakem jako rovnotlaké stupně [7, s. 191].

12.795 Příklad i-s diagramu Curtisova stupně

Jedna z možných konstrukcí Curtisova stupně je uvedena v kapitole Stupně parních turbín.

Návrh axiálního přetlakového stupně turbíny

Přetlakové stupně s přímými lopatkami se používají u tepelných turbín a turbokompresorů případně dmychadel. Lze je také použít u větrných turbín, tam kde není důležitá co nejvyšší účinnost ale jednoduchost, více o takovém stupni v kapitole Zjednodušený aerodynamický návrh větrné turbíny.

U axiálních přetlakových stupňů je výhodný stupeň reakce ρ=0,5. Při takové reakci jsou nejnižší profilové ztráty, protože rychlosti c₁ a w₂ jsou stejné nebo velmi podobné navíc je možné použít symetrickou geometrii a tvar lopatek pro statorovou i rotorovou řadu lopatek, což je výrobně výhodné. Odtud plyne i symetrický tvar rychlostního trojúhelníku pro statorovou a rotorovou řadu lopatek:

13.353 Válcový řez přetlakovým stupněm a jeho rychlostní trojúhelník

Jedna z možných konstrukcí axiálního přetlakového stupně je uvedena v kapitole Stupně parních turbín. Při stupni reakce kolem ρ=0,5 už se výrazně projevuje na obvodové práci i rozdíl relativních rychlostí:

14.354 i-s diagram přetlakového stupně

Podobně jako u rovnotlakého a Curtisova stupně i pro přetlakový stupeň s ρ=0,5 lze nalézt optimální rychlostní poměr, při kterém dosahuje maximální obvodové účinnosti:

15.355 Přibližné optimální parametry přetlakového axiálního stupně tepelné turbíny

Axiální přetlakový stupeň tepelné turbíny je při φ≈1, cos α₁≈1 a stejné obvodové rychlosti schopen optimálně zpracovat přibližně poloviční entalpický spád než axiální rovnotlaký stupeň viz porovnání Rovnice 9. a Rovnice 15., respektive poměr optimálních entalpických spádů v axiálním přetlakovém stupni ku axiálním rovnotlakém stupni ku dvouvěncovém Curtisovu stupni je přibližně 1:2:8. Dále rovnotlaké kanály jsou více citlivé na odtržení proudu od profilu při změně průtoku.

Návrh axiálního přetlakového stupně kompresoru

U přetlakových stupňů kompresorů a dmychadel se také využívá výhod stupně reakce ρ=0,5 pro normální stupeň (c₁=c₃):

16.1101 Rychlostní trojúhelník axiálního kompresorového stupně

Axiální stupeň kompresoru se obvykle navrhuje tak, aby obvodová složka absolutní rychlosti na vstupu do stupně byla co nejmenší, což vede na optimální obvodové účinnosti. Při návrhu kompresorového stupně se používá velmi často T-s diagram místo i-s digramu. To je dáno především tím, že turbokompresory stlačují obvykle směs plynů, pro kterou lze pomocí porovnávací izobary zkonstruovat T-s diagram. Samozřejmě pokud je znám i-s diagram komprimovaného plynu lze použít ten, převod je triviální. Při samotném výpočtu se jednotlivé body v T-s diagramu stanovují analyticky pomocí rovnic pro ideální tekutinu především rovnic pro vratné termodynamické změny a rovnice pro rozdíl entalpií mezi dvěma stavy s tím, že se dosazují střední hodnoty termomechanických vlastností pracovního plynu. Následovně se skutečné stavy plynu v jednotlivých bodech korigují pomocí skutečného T-s nebo i-s diagramu. Tento postup je možný, protože v axiální kompresorové stupně jsou málo zatížené a změny stavu ve stupni nejsou velké. V T-s diagramu se kinetická energie pracovního plynu projeví zvýšením teploty celkového stavu o tzv. teplotní ekvivalent rychlosti:

17.1121 T-s diagram průběh komprese ve stupni axiálního turbokompresoru

Kuželové stupně s přímými lopatkami

U tepelných turbín a turbokompresorů dochází během pracovního procesu ve stroji ke změnám hustoty pracovního plynu. Při stejných průtočných průřezech se u kompresorových stupňů postupně rychlosti snižují a u turbínových naopak. Pro zachování co nejvyšší účinnosti všech stupňů u vícestupňových strojů je nutné postupně zvětšovat délku lopatek nebo ještě lépe měnit referenční poloměr lopatek či kombinace obou:

18.922 Hlavní způsoby přizpůsobení geometrie stupňů s přímými lopatkami na změnu hustoty pracovního plynu

Případ (a) má výhodu v konstrukční jednoduchosti (nezvětšuje průměr turbíny). Nevýhodou je, že se zvyšuje poměr l·r^-1. Tato varianta se používá pro skupiny s menším počtem rovnotlakých stupňů a Curtisova stupně.

Případ (b) je typický pro malé průmyslové parní turbíny s protitlakem. Nárůst objemu je kompenzován pouze zvyšováním referenčního poloměru, takže délka lopatek zůstává stejná. Výhodou je že poměr l·r^-1 klesá.

Případ (c) se od předchozího liší v tom, že se mění délka lopatek, ale geometrie lopatek se nemění. Zvyšování délky lopatek by mělo být takové, aby poměr l·r^-1 byl nejhůře konstantní. Používá se u průmyslových parních turbín s nízkým protitlakem je možná samozřejmě varianta ε_h=0.

Případ (d) je typický pro poslední stupně axiálních turbokompresorů. Mění se délka lopatek a poměr l·r^-1 se snižuje.

Jestliže jsou lopatky přímé je výhodné, aby geometrie všech lopatek ve skupině stupňů byla stejná, respektive aby úhly v rychlostním trojúhelníku byly stejné (navržené pro střední poloměr skupiny stupňů), v takovém případě totiž bude lopatkování nejméně nákladné. Stupně (jejich geometrie) jsou navrženy jako axiální, ale přesto v energetické bilanci již nelze zanedbávat změnu obvodových složek, což má vliv na stupeň reakce a velikosti rychlostí:

19.1029 Možnosti stupňů s přímými lopatkami a se změnou referenčního poloměru

i-s diagramy stupňů se změnou referenčního poloměru jsou tedy podobné diagramům pro radiální stupně s tím rozdílem, že se prakticky vůbec na nich neprojevuje vliv ventilačních ztrát.

Stupně se zkroucenými lopatkami

Jak bylo zmíněno v úvodu tohoto článku rychlostní trojúhelník se po výšce lopatky mění v důsledku změny obvodové rychlosti, změny obvodové složky absolutní rychlosti a v důsledku změny tlaku po výšce lopatky⁽⁹⁾. Těmto změnám se musí přirozeně přizpůsobovat i geometrie profilu lopatek, pokud chceme dosáhnout maximální vnitřní účinnosti stupně. Proto se následující kapitoly zabývají základním popisem prostorového osově symetrického proudění ideální tekutiny, ze kterého je možné vycházet při návrhu a konstrukci stupně lopatkového stroje se zkroucenými lopatkami. Cílem takového návrhu je určení geometrie lopatek na jednotlivých poloměrech pomocí tvaru rychlostních trojúhelníků. To znamená vypočítat jak se mění jednotlivé rychlosti a i-s diagramy po výšce lopatek tj. v radiálním směru.

⁽⁹⁾Poznámka

V objemu proudící tekutiny, která proudí po křivkách vzniká podle Eulerovy n-rovnice ve směru normály gradient tlaku. Především u delších lopatek vzhledem ke střednímu průměru lopatkové řady může být rozdíl tlaků v mezeře lopatkovými řadami mezi patou a koncem lopatky tak velký, že se významně změní termodynamické poměry (stupeň reakce či u plynů výrazně i hustota) na jednotlivých průměrech stupně:

20.676 Gradient tlaku v mezeře mezi statorovou a rotorovou řadou turbíny a jeho důsledky

Obecné rovnice a předpoklady řešení prostorového proudění ve stupni lopatkového stroje

Energetickou bilanci stupně lze stanovit v jakémkoliv místě stupně pomocí rovnic pro První zákon termodynamiky pro otevřený systém v diferenciálním tvaru. Vzhledem ke složitosti proudění viskózní tekutiny se ztrátami je tato rovnice řešitelná se standardní přesností pouze numericky, například metodami konečných prvků (musí být známa geometrie lopatek stupně a vlastnosti pracovní látky). Při výpočtu se samozřejmě uvažuje s menší či větší mírou vlivu profilových i ostatních ztrát, podle toho co se výpočtem zkoumá. Návrh pro jmenovité parametry stupně se provádí pro ustálené proudění, ale modelováním lze zjistit i přibližné chování při změně průtoku. Více o možnostech tvorby numerického modelu proudění ve stupni lopatkového stroje v [5, s. 8-1].

Pro základní návrh geometrie lopatek se používá relativně velké množství analytických postupů, podle toho o jaký typ stupně se jedná, podle zatížení, vlastností pracovní tekutiny, podle toho jaké by měl mít stupeň vlastnosti atd.⁽¹⁰⁾. Každý takový návrh by měl více či méně respektovat přirozené chování pracovní tekutiny při osově symetrickém proudění. Především se jedná o vznik příčného tlakového gradientu, takže geometrie stupně by měla být navržena optimálně tak, aby se na každém poloměru měnil stupeň reakce – tzv podmínka radiální rovnováhy. Pokud takové chování návrh respektovat nebude, bude docházet ke ztrátám způsobených vířením pracovní tekutiny, která se bude chovat jinak než očekával návrh.

Návrh stupně se zkroucenými lopatkami je velmi podobný návrhu stupně s přímými lopatkami s tím, že se provádí na více poloměrech nejen na tom referenčním. Klíčem kvalitního návrhu je nalezení souvislostí mezi jednotlivými proudovými plochami, tak aby se dal odvodit rychlostní trojúhelník na všech poloměrech z rychlostního trojúhelníku na sousední proudové ploše. Nejčastěji se při hledání souvislostí mezi jednotlivými proudovými plochami stupně vychází z toho, že reálné proudění je velmi blízké proudění potenciálnímu. To znamená, že změna rychlostí v jednotlivých prostorových směrech by měla být taková, aby rotor rychlosti byl co nejblíže nule. Obecnou rovnici pro rotaci rychlosti ve válcové soustavě souřadnic lze zjednodušit pro osově symetrické proudění ve stupni, při kterém jsou veškeré derivace v obvodovém směru rovny nule (platí pro ideální proudění v mezerách mezi lopatkovými řadami):

21.705 Rotor rychlosti pro osově symetrické potenciální proudění

Z rovnice pro rotor rychlosti je evidentní, že podmínku potenciálního proudění lze mimo jiné splnit, jestliže součin r·c_u v radiálním směru bude konstantní. Součin r·c_u se nazývá v hydrodynamice cirkulace rychlosti. Jestliže má být cirkulace rychlosti po výšce lopatek stejná, potom i obvodová práce musí být stejná. Tento závěr plyne z porovnání rovnic pro obvodovou práci a rovnice cirkulace rychlosti. Podmínku konstantní obvodové práce po výšce lopatky lze dodržet pouze při izoentropickém proudění stupněm, protože při proudění se ztrátami budou ztráty po výšce lopatky různé (největší jsou u paty a špice nejmenší na středním poloměru).

Při základním návrhu se stupeň navrhuje jako by proudění bylo beze ztrát pro l_Eiz a nebo mnohem častěji pro obvodovou práci l_Eref, která je nižší než l_Eiz o předpokládané ztráty. Velikost l_Eref se snaží respektovat očekávaný průběh obvodové práce alespoň v okolí středního poloměru lopatky, kde je obvodová práce přibližně konstantní. Používají se ale i takové návrhy, které ještě více respektují očekáváný průběh obvodové práce tím, že průběh obvodové práce aproximují nějakou funkcí (nejčastěji exponenciální [5, s. 5-8]). Takový návrh už samozřejmě nerespektuje podmínku potenciálního proudění, ale výsledek je blíže reálným parametrům stupně:

22.434 Základní návrhy průběhu obvodové práce na jednotlivých poloměrech stupně lEiz [J·kg-1] průběh obvodové práce při proudění beze ztrát (potenciální); lEref [J·kg-1] navrhovaný lienární (konstantní) průběh obvodové práce částečně respektující skutečný průběh obvodové práce; lEex [J·kg-1] navrhovaný exponenciální průběh obvodové práce(11) částečně respektující skutečný průběh obvodové práce; n [-] exponent (navrhuje výpočtář stupně – hodnota n=-1 vede na konstantní průběh obvodové práce), a, b konstanty, které se odvodí z předpokládaného průběhu obvodové práce. Obrázek je nakreslen pro axiální stupeň turbíny, ale pro axiální stupeň pracovního stroje platí to samé, akorát obvodová práce bude záporná.

Pro základní návrh odhad průběhu obvodové práce nestačí, je nutné ještě navrhnout změnu axiální složky rychlosti po výšce lopatky. Pro axiální složku rychlosti existují dva hlavní způsoby předpisu. Nejednoduší na výpočet je navrhnout stupeň pro konstantní složku axiální rychlosti c_a(r)=konst. Druhou možností je navrhnout stupeň tak, aby na každé proudové ploše byl stejný měrný průtok (hmotnostní průtok na mm² průtočné plochy):

23.707 Princip návrhu stupně s konstantním měrným průtokem v [m3·kg-1] měrný objem pracovního plynu. Jedná se o axiální turbínový stupeň s předepsanými válcovými plochami, pracovní tekutinou je plyn. I když na vstupu i výstupu ze stupně může být po výšce lopatek stejná axiální rychlost, tak mezi lopatkovými řadami se musí měnit. Má-li zůstat průtok na každém poloměru konstantní (průtočný průřez zůstává zachován) musí se snižovat rychlost, protože vlivem růstu stupně reakce se snižuje měrný objem.

Je zřejmé, že stupně navržené pro c_a(r)=konst. budou podle Rovnice 21lépe vyhovovat předpokladu potenciálního proudění. Jenže toho lze u stlačitelného proudění dosáhnout pouze odklonem proudnic, tak jak je naznačeno na Obrázku 24, tak aby axiální rychlost byla stejná u špice i paty lopatky. Tento odklon je způsoben poklesem měrného objemu na vnějším poloměru lopatek. Ve výsledku to znamená, že většina pracovního plynu bude protékat blíž k vnějšímu poloměru lopatek. Toto chování má neblahý vliv při zmenšení průtoku stupněm, při kterém se mohou proudnice u hřídele odtrhávat za vzniku ztráty zpětným prouděním:

24.709 Proudění axiálním stupněm při velké změně měrného objemu pracovního plynu vlevo při jemenovitých parametrech; vpravo vznik zpětného proudění u dlouhé zkroucené lopatky při zmenšení průtoku stupněm – tímto druhem ztrát jsou zejména ohroženy poslední stupně vícestupňových lopatkových strojů [7, s. 161].

Axiální stupeň s konstantním měrným průtokem splňuje podmínku potenciálního proudění jen při nestlačitelném proudění (nemění se měrný objem ve stupni). Při stlačitelném proudění tuto podmínku sice nesplňují, ale mívají větší účinnosti mimo návrhový stav stupně především při sníženém průtoku, protože průtok stupněm je rovnoměrněji rozložený.

V následujících kapitolách uvádím příklady postupů základních návrhů jednotlivých typů axiální a kuželových stupňů s přihlédnutím k prostorovému charakteru proudění.

Návrh stupně s  konstantní obvodovou prací

V případě čistě axiálního vstupu i výstupu ze stupně (c_0u=c_2u=0 m·s^-1 pro turbínové stupně, c_1u=c_3u=0 m·s^-1 pro stupně pracovních strojů) budou mít rychlostní trojúhelníky na každém poloměru tvar odpovídající Obrázku 5. Kompletní rychlostní trojúhelník na každém poloměru se vypočítá tak, že se navrhne vstupní a výstupní rychlost ze stupně a vypočítá stupeň reakce.

V případě nestlačitelného proudění lze stanovit stupeň reakce pomocí vzorce:

25.1005 Stupeň reakce po výšce lopatky axiálního stupně s konstantní obvodovou prací

Stupeň reakce pro každý poloměr pro případ konstantního měrného průtoku a při změně hustoty se musí spočítat iteračně:

26.526 Iterační výpočet stupně reakce axiálního stupně na vyšetřovaném poloměru

Axiální stupeň s konstantní cirkulací se používá prakticky u všech typů axiálních stupňů tzn. od vodních strojů (turbíny i čerpadla) přes ventilátory, vrtule až po stroje tepelné (turbíny i kompresory). Pro tento typ stupně je charakteristické silné zkroucení rotorové i statorové řady lopatek. Nejvyšší energetické zatížení je u tohoto stupně dosaženo, jestliže je u paty lopatky nulový stupeň reakce.

Podmínku konstantní obvodové práce po výšce lopatek lze u turbín splnit i pro případ c_2u≠konst. V takovém případě musí být obvodové složky rychlosti před a za rotorem takové, aby byla splněna podmínka r·c_1u-r·c_2u=konst. Tu lze splnit předpokladem konstantní cirkulace rychlosti po výšce lopatky před i za rotorovou řadou lopatek (r·c_1u=konst., r·c_2u=konst.), nebo jakýmkoliv jiným předpisem průběhu obou cirkulací takovým způsobem, aby jejich rozdíl byl konstantní – například exponenciální průběh obou cirkulací se stejnými konstantami⁽¹²⁾:

27.381 Vlastnosti stupně s konstantní obvodovou prací a exponenciální cirkulací rychlosti

Problémem stupně s nenulovou obvodovou složkou na obou stranách rotorové řady lopatek je v tom, že se mění i tlak po výšce lopatky (na výstupu z turbínového stupně; na vstupu do stupně pracovního stroje).

Návrh stupně s proměnlivou obvodovou prací

Existuje větší množství možností jakým způsobem predikovat změnu obvodové práce po výšce lopatky, jak naznačuje Obrázek 22, ale zde se budu zabývat pouze případem exponenciální změny obvodové práce.

Postup návrhu takového stupně je velmi podobný postupu při návrhu stupně s konstantní obvodovou prací. Opět se obvykle používá předpoklad čistě axiálního vstupu i výstupu ze stupně.

28.383 Stupeň reakce po výšce lopatky axiálního stupně s exponenciální změnou obvodové práce

Stupeň reakce pro každý poloměr pro případ konstantního měrného průtoku a při změně hustoty lze spočítat iteračně stejným postupem jako v případě návrhu stupně s konstantní obvodovou prací. Při návrhu se v prvním přiblížení předpokládá konstantní výstupní rychlost ze stupně.

Exponenciální průběh cirkulace rychlosti způsobuje, že úhel relativní rychlosti se mění tak, že na špici lopatky může být velmi blízký úhlu u paty lopatky, i když ve středu lopatky je značně rozdílný. U takových lopatek se méně projevuje ztráta sekundárním prouděním. To je dáno tím, že právě ztráta sekundárním prouděním je dána nerespektováním rozdílu profilových ztrát při návrhu stupně s konstantní obvodovou prací.

29.710 Lopatka s exponenciálním průběhem obvodové práce Porovnejte tvar s lopatkou na Obrázku 20, která byla navržena pro konstantní cirkulaci rychlosti. Takovému tvaru lopatky se říká prohnutá zkroucená lopatka (blowed-twisted blade nebo 3D stacks).

Kuželový stupeň s konstantní obvodovou prací

Při stlačitelném proudění se postupně zvyšuje axiální rychlost na výstupu ze stupně, které lze kompenzovat i změnami patního i obvodového poloměru lopatek po jednotlivých stupních nebo po skupinách stupňů. Výhodou tohoto řešení je, že geometrie lopatek je pro všechny stupně stejná, pouze se opakuje na jiném průměru (pokud se nejedná o poslední turbínový stupeň s kritickým průtokem):

30.683 Provedení odstupňované změny průtočného průřezu u axiálních stupňů

Nevýhodou odstupňování jsou přechodové části mezi jednotlivými skupinami, nárůst hmotnosti hřídele i počtu lopatek umístěných po obvodě a velký výstupní průměr. Alternativou k takové konstrukci je model proudění po kuželových plochách.

Kuželový stupeň s konstatní obvodovou prací v podstatě splňuje stejné podmínky jako předchozí axiální stupeň tj. c_0u=c_2u=0 m·s^-1, respektive c_1u=c_3u=0 m·s^-1. Navíc by se délka lopatek měla měnit s hustotou plynu tak, aby vstupní i výstupní rychlost ze stupně byla stejná c₀=c₂ pro stupně turbín a c₁=c₃ pro stupně pracovních strojů:

31.712 Kuželový stupeň s konstantní cirkulací t [m] délka stupně. Příklad proudění po čistě kuželových plochách ve stupni turbíny.

Je evidentní, že na každém poloměru se bude měnit sklon kuželové plochy ε (v tomto případě se s poloměrem zvětšuje). Proto se na každém vstupní nebo výstupním poloměru musí měnit i axiální a radiální složka absolutní rychlosti (c_a(r)≠konst., c_r(r)≠konst.). Podstatné ale je, že na konkrétní kuželové ploše zůstávají tyto složky konstantní. Odtud lze pro konstantní axiální složku rychlosti z rovnice kontinuity odvodit jednoznačný vztah mezi vstupním a výstupním poloměrem:

32.711 Vzorec pro výpočet výstupního poloměru kuželového stupně v [m3·kg-1] měrný objem pracovního plynu. V případě pracovních strojů se označuje stav před stupněm místo 0 číslem 1 a za stupněm místo 2 číslem 3. Odvození rovnice je v Příloze 711.

Posledním vzorcem je dán jednoznačný vztah mezi axiální a radiální složkou rychlosti, protože z délky stupně t lze vypočítat úhel kuželové plochy ε. Kuželový stupeň zohledňuje změnu měrného objemu a již z principu tedy by měl být navržen pro konstantní měrný průtok. Znaméná to, že axiální složka rychlosti by ve směru radiálním měla být proměnná, a protože ve směru axiálním se mění i radiální složka tak se takový návrh blíží předpokladům potenciálního proudění.

33.714 Vzorec axiální složky rychlosti kuželového stupně s konstantním měrným průtokem

Stupeň reakce se opět musí počítat iteračně:

34.496 Iterační výpočet stupně reakce axiálního stupně na vyšetřovaném poloměru

Výše uvedený typ kuželového stupně je pouze jeden z mnoha možných variant. Například v [7, s. 166], [11] se sklon kuželových ploch předepisuje a následně iteračně dopočítává vstupní a výstupní rychlost ze stupně, které se po výšce lopatky mění. Další možnosti kuželových proudových ploch jsou následující:

35.879 Nejčastější provedení kuželových stupňů a stupeň reakce kuželového stupně

U vícestupňových lopatkových strojů lze na jedné hřídeli jednotlivé typy stupňů i kombinovat. Například u parní turbíny mohou být první stupně s prizmatickými lopatkami, potom následují axiální stupně se zkroucenými lopatkami a poslední stupně mohou být kuželové.