Ztráty ve Stirlingových motorech

Výkon Stirlingova motoru na hřídeli ovlivňují ztráty. Tyto ztráty lze rozdělit na termodynamické a mechanické. Termodynamické ztráty přímo ovlivňují tvar p-V diagramu, mezi mechanické patří tření v mechanismech motoru (v ložiscích, pístních kroužků o válec apod). Také vznikají jiné ztráty, které nemusí ovlivňovat práci motoru, ale ovlivňují například spotřebu paliva či tepla (účinnost zdroje tepla, vedení tepla v bloku motoru apod.), tento druh ztrát je podrobně popsán v [5, s. 105].

Podobnosti Stirlingových motorů

Pro přibližný návrh Stirlingova motoru lze využít teorii podobnosti podobně jako při návrhu jiných strojů (viz článek Podobnosti lopatkových strojů). Nejpoužívanějším podobnostním kritériem Stirlingova motoru je Bealevo číslo*, pomocí kterého lze predikovat výkon motoru (existují i jiná podobnostní čísla Stirlingových motorů například více zohledňující teplotu pracovního plynu na studené straně, ale příliš se nepoužívají). Na začátku výpočtu je nutné znát pouze maximální (zdvihový) objem motoru na teplé straně, předpokládané otáčky, střední tlak pracovního plynu v motoru a teplotu ohříváku (vnější povrch):

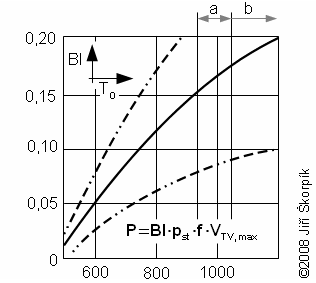1.854 Bealeovo číslo jako funkce střední teploty pracovního plynu na teplé straně motoru. Bl [-] Bealovo číslo; P [W] výkon Stirlingova motoru na hřídeli; f [Hz] počet cyklů uskutečněných za sekundu; pst [MPa] střední tlak pracovního plynu v motoru; TT,st [K] teplota ohříváku motoru; VTVmax [cm3] zdvihový objem válce na teplé straně motoru. a hranice mezi běžnými legovanými a vysoce legovanými oceli vhodné pro ohřívák Stirlingova motoru; b přechod mezi vysoce legovanými materiály a materiály keramickými. Graf je vytvořen pro teplotu chladiče 65 °C a lze ho použít pro všechny typy Stirlingových motorů a druhy pracovního plynu.

*Bealeovo číslo

Metodu popsal Walker Graham v roce 1979 v [2], [3, s. 57]. Pojmenována byla podle Williama Beala, který jako první podobnosti mezi motory všiml během svého působení ve firmě Sunpower (USA; Ohio; Athens), kde prováděl vyhodnocení měření Stirlingových motorů (více o historických souvislostech metody v [5, s. 99]).

U motorů s menším mrtvým objemem a nízkou teplotou pracovního plynu v chladiči se velikost Bealova čísla blíží horní čerchované čáře, a naopak u motorů s velkým mrtvým objemem a vysokou teplotou pracovního plynu v chladiči se velikost Bealova čísla blíží spodní čerchované čáře.

Termodynamické ztráty oběhu Stirlingova motoru

Oběh Stirlingova motoru nejvíce ovlivňují ztráty netěsností pístních kroužků, ztráty vedením tepla z  pracovního plynu do/z okolí a vedením tepla v matrici regenerátoru, a tlakové ztráty vznikající při proudění pracovního plynu. Čím větší jsou tyto ztráty tím je skutečný oběh motoru rozdílnější od ideálního/porovnávacího oběhu. K výpočtu reálného oběhu Stirlingova motoru se používá analytický nebo numerický postup:

Analytický výpočet

V tomto případě se nejprve vypočítá p-V diagram oběhu Stirlingova motoru pro případ konstantní hodnoty exponentu polytropy podle rovnic uvedených v článku Oběh Stirlingova motoru. Tento diagram už zahrnuje některé typy ztrát, které je jinak nutné odečítat v případě použití Schmidtovy idealizace; [5, s. 71]; [3, s. 40] (především se jedná o ztráty spojené s rozdílem skutečných dějů oproti izotermickým, které Schmidtova idealizace předpokládá). V druhém kroku se tvar p-V diagramu zpřesní podle očekávané netěsnosti pístních kroužků, která má významný vliv (popis je uveden níže). Práci a účinnost motoru lze zpřesnit započítáním dalších ztrát například podle [5, s. 105], [3].

Numerický výpočet (CFD model)

Spočívá v zahrnutí reálných podmínek (součinitele přestupu tepla; změny termomechanických vlastností pracovního plynu) a tedy i ztrát (ztráty vedením tepla do okolí; tlakové ztráty; ztráty netěsností pístních kroužků) přímo do výpočtu oběhu motoru. Tato metoda je náročná na sestavování počátečních a okrajových podmínek a stále činí problémy některé ztráty zahrnout kvůli konvergenci řešení. Jeden z prvních, kdo vytvořil kompletní numerický model Stirlingova motoru včetně spalovacího zařízení byl Khamid Mahkamov, tento model zároveň ověřoval na vyrobeném motoru (γ-modifikace, 0,5 kW) [1, s. 96].

Tento článek dále popisuje pouze konstrukci p-V diagramu pro případ analytického výpočtu. Ze zkušeností i z měření jednoznačně plyne, že největší vliv na změnu tvaru p-V diagramu má exponent polytropy a ztráta netěsností pístních kroužků (deformuje p-V diagram ze všech stran). Vliv dalších ztrát* na tvar p-V diagramu lze zanedbat. I tak je výsledný výpočet dostatečně přesný pro dimenzování konstrukce Stirlingova motoru.

Ztráta netěsností pístních kroužků

Netěsnost pístních kroužků je obvykle největší ztrátou výkonu Stirlingova motoru jak naznačují praktické zkušenosti s provozem. Často se jedná o hlavní technologický problém při vývoji nového motoru. K netěsnosti pístních kroužků dochází kvůli drsnosti povrchu válce pístního kroužku, rozdílu průměru válce a kroužku a v důsledku vibrací při chodu stroje.

Pístní kroužky jsou na pístech na teplé i studené straně motoru. Pístní kroužky oddělují pracovní objem motoru od objemu pod písty. Objem pod písty může podle typu modifikace motoru sloužit jako vyrovnávací prostor nebo může být dalším pracovním prostorem v případě dvojčinné modifikace motoru. Tlak se v pracovním objemu motoru během jednoho cyklu výrazně mění. V případě, že prostor pod písty není pracovní, potom by měl být tak velký, aby zde byl tlak přibližně konstantní. Netěsnostmi v pístních kroužcích uniká pracovní plyn do prostoru pod písty, když nad pístem je tlak vyšší než pod ním a obráceně. To znamená, že hmotnost pracovního plynu v pracovním objemu motoru není konstantní.

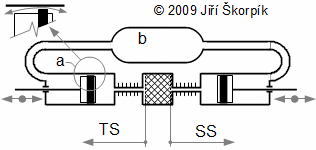2.476 Schéma Stirlingova motoru α-modifikace. a pístní kroužek; b prostor pod pístem propojený s vyrovnávací nádrží; TS teplá strana motoru; SS studená strana motoru. Obrázek ukazuje střídavý únik pracovního plynu přes netěsnost pístních kroužků mimo pracovní objem a zpět.

Hmotnost pracovního plynu v motoru se během jednoho oběhu mění mezi maximálním a minimálním množstvím. Oběh lze tedy rozdělit na dvě části. V první části oběhu se množství pracovního plynu snižuje (pracovní plyn proudí netěsnostmi z pracovního objemu) a v druhé zvyšuje (pracovní plyn proudí netěsnostmi do pracovního objemu). Tato změna množství pracovního plynu má dopad na tvar p-V diagramu. Přesněji řečeno se sníží maximální tlak oběhu a zvýší minimální tlak oběhu oproti případu dokonale těsných pístních kroužků. Změna tlaku není obvykle tak velká, ale přesto se vnitřní práce Strilingova motoru může výrazně snížit. Toto významné snížení je způsobeno posunutím maximální hodnoty tlaku více doleva v p-φ diagramu. To znamená, že maximální tlak nastane dříve než v případě dokonale těsných pístních kroužků:

3.223 Vliv netěsnosti pístních kroužků na tvar p-φ diagramu*.

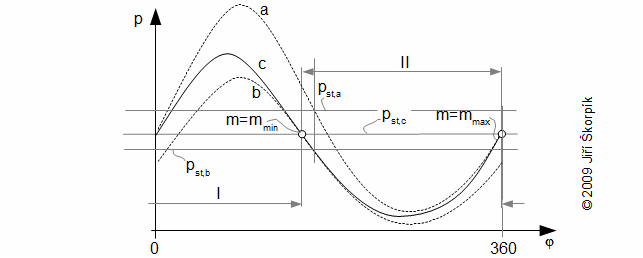
Netěsnost pístních kroužků je definována jako poměr maximální změny hmotnosti pracovního plynu a hmotnosti pracovního plynu v pracovním objemu motoru pro případ dokonale těsných pístních kroužků:

4.231 Hmotnostní poměr.

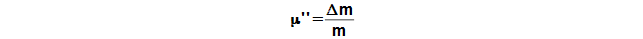
Při porovnávání naměřeného p-φ diagramu s výpočteným podle postupu uvedeného v článku Oběh Stirlingova motoru byla zjištěna podobnost [7, s. 63]. Naměřený průběh tlaku byl tvarem podobný vypočítanému, ale posunutý o určitou diferenci Δφ a zploštělý v extrémech tlaku o Δp. Na základě těchto poznatků byly vytvořeny zjednodušující podmínky řešení oběhu Stirlingova motoru s netěsnými pístními kroužky: (1) Tlak ve Stirlingově motoru pro případ dokonale těsných pístních kroužků (ideální oběh). (2) Tlak plynu pod písty je konstantní a odpovídá střednímu tlaku v pracovním objemu motoru. (3) Netěsnost pístních kroužků způsobuje posun ideálního oběhu o úhel Δφ. (4) Změna tlaku je přímo úměrná úbytku pracovního plynu v motoru (lineární model). (5) Rozdíl tlaku (mezi maximálním/minimálním tlakem pro případ oběhu s dokonalou těsností pístních kroužků a oběhem pro netěsné pístní kroužky) je ekvivalentní poloviční hodnotě Δm. (6) Pracovní plyn uniká z pracovního objemu pouze přes pístní kroužky. (7) Únik pracovního plynu není tak velký, aby ovlivňoval střední teplotu pracovního plynu v pracovním objemu a exponent polytropy. (8) Oběh je ustálený.

Je-li tlak funkcí pootočení hřídele p(φ) potom průběh tlaku posunutý o Δφ je funkcí pootočení a posunutí p'(φ+Δφ). Posunutí Δφ je možné vypočítat z bodu minimálního množství pracovního plynu v pracovním objemu motoru:

5.483 Posunutí průběhu tlaku a jeho vliv na tvar p-V diagramu.

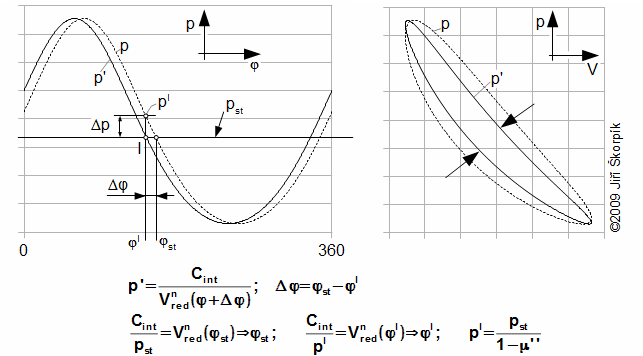
Rovnice objemu V_red závisí na typu mechanismu pístu. Nejčastěji se používá u Stirlingových motorů klikový mechanismus a v takovém případě lze, za jistých podmínek, odvodit rovnici pro výpočet Δφ přímo:

6.238 Zjednodušené rovnice pro výpočet Δφ.

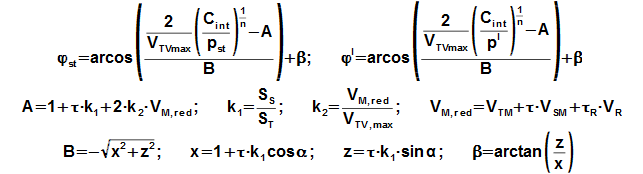
Střídavá změna hmotnosti pracovního plynu v pracovním objemu způsobuje i pokles tlakového poměru. Podle zjednoduujícího předpokladu (4) je změna tlaku přímo úměrná změně hmotnosti pracovního plynu:

7.484 Změna tlaku a jeho vliv na průběh p-φ diagramu a p-V diagramu.

Úloha 1: souhrn zadání a výsledků.

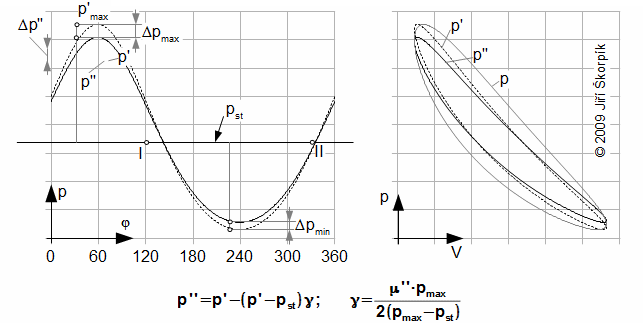
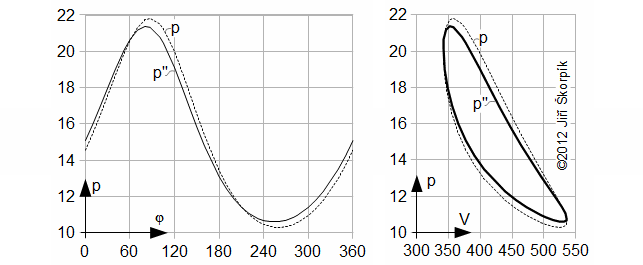
Je evidentní, že opotřebení pístních kroužků bude způsobovat významné snížení vnitřní práce motoru, proto je účelné vytvořit závislost vnitřní práce motoru na hmotnostním poměru μ'' z pracovního objemu motoru podobně jako je tak učiněno v následující úloze:

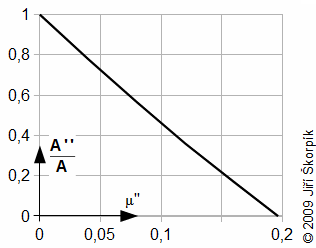Úloha 2: souhrn zadání a výsledků. A [J] vnitřní práce motoru pro případ dokonale těsných pístních kroužků; A'' [J] vnitřní práce motoru s netěsnými pístními kroužky.

Z výsledku poslední úlohy je patrné, že vliv netěsnosti pístních kroužků na práci oběhu je vysoký. Již při úniku plynu o 13% se sníží vnitřní práce motoru o 50%, při úniku okolo 20 % je motor prakticky neprovozuschopný. Netěsnost je závislá na drsnosti povrchu válce, deformaci pístního kroužku a vibrací motoru. Velikost netěsnosti lze přibližně vypočítat z rovnice pro hmotnostní tok plynu tryskou:

8.887 Přibližný výpočet průtoku plynu netěsností.

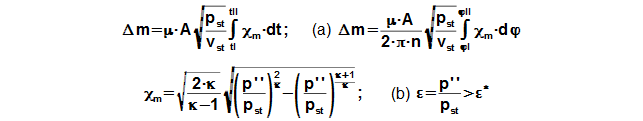
Protože oblast pístních kroužků je chlazena a teplota pracovního plynu pod písty je přibližně konstantní není nutné v takových případech provádět výpočet pro každý pístní kroužek samostatně.

Z Rovnice 8 plyne i závislost hmotnostního průtoku na měrném objemu pracovního plynu, respektive teplotě. Plyn na teplé straně, který proudí netěsností pístních kroužků pod píst je teplejší než plyn, který proudí touto netěsností zpět. To způsobuje, že v části II oběhu vnikne do pracovního prostoru více plynu než z něj uniklo v části oběhu I. Proto se do pístu vyvrtává malá díra/tryska* (o průměru několik desetin mm-podle velikosti V_TVmax, druhu plynu a tlakovém poměru), která zvýší únik plynu a zároveň vytváří rovnováhu mezi únikem a návratem pracovního plynu. Na studené straně je situace přesně opačná, ale rozdíl teplot není tak velký a nerovnováha na teplé straně hmotnostní bilance převažuje.

Uvedený postup návrhu oběhu Stirlingova motoru pro případ netěsností pístních kroužků vychází z měření na experimentálních motorech z let 2002 až 2012. Tyto experimenty prováděla společnost Tedom a.s. [4], respektive společnost Strojírny Bohdalice, a.s. [6], která v roce 2010 vývoj Stirlingových motorů převzala. Projekt v té době vedl Josef Brož. Některá měření jsou dostupná v [7].

Odkazy

Bibliografická citace článku

ŠKORPÍK, Jiří. Ztráty ve Stirlingových motorech, Transformační technologie, 2009-07, [last updated 2012-10]. Brno: Jiří Škorpík, [on-line] pokračující zdroj, ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/seznam-clanku.html#36. English version: Losses in Stirling engines. Web: https://www.transformacni-technologie.cz/en_seznam-clanku.html#36.